Omo dėsnis grandinės atkarpai
Pagrindinis elektrotechnikos dėsnis, kurį galite naudoti tirdami ir skaičiuodami elektros grandines, yra Ohmo dėsnis, nustatantis ryšį tarp srovės, įtampos ir varžos. Būtina aiškiai suvokti jos esmę ir mokėti ją teisingai panaudoti sprendžiant praktines problemas. Elektros inžinerijoje dažnai daromos klaidos dėl nesugebėjimo teisingai taikyti Ohmo dėsnio.
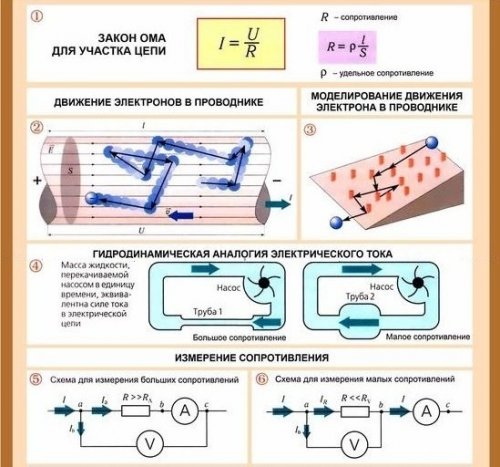
Omo dėsnis grandinės atkarpai: srovė yra tiesiogiai proporcinga įtampai ir atvirkščiai proporcinga varžai.
Jei elektros grandinėje veikianti įtampa padidinama kelis kartus, srovė toje grandinėje padidės tiek pat. Ir jei kelis kartus padidinsite grandinės varžą, srovė sumažės tiek pat. Lygiai taip pat vandens srautas vamzdyje yra didesnis, tuo stipresnis slėgis ir mažesnis vamzdžio pasipriešinimas vandens judėjimui.
Populiaria forma šis dėsnis gali būti suformuluotas taip: kuo didesnė įtampa esant tokiai pačiai varžai, tuo didesnė srovė, ir tuo pačiu, kuo didesnė varža tai pačiai įtampai, tuo mažesnis srovės stiprumas amperais.
Norint matematiškai išreikšti Omo dėsnį kuo paprasčiau, laido, kuriuo teka 1 A srovė, esant 1 V įtampai, varža laikoma 1 omai.
Srovę amperais visada galima nustatyti padalijus įtampą voltais iš varžos omais. Todėl Omo dėsnis grandinės atkarpai parašytas tokia formule:
I = U / R.
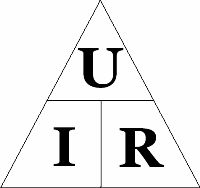
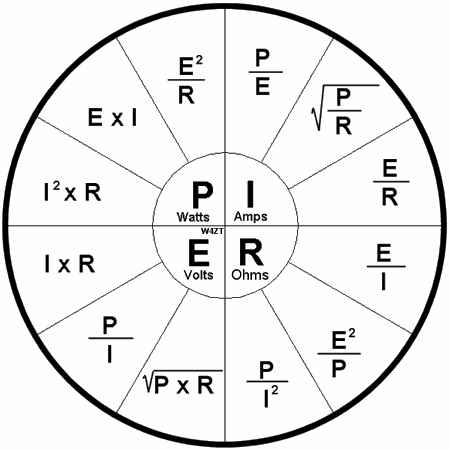
Magiškas trikampis
Bet kuri elektros grandinės dalis ar elementas gali būti apibūdinamas trimis charakteristikomis: srovė, įtampa ir varža.
Kaip naudoti Ohmo trikampį: uždarome reikiamą reikšmę - kiti du simboliai parodys jo skaičiavimo formulę. Beje, tik viena formulė iš trikampio vadinama Ohmo dėsniu – ta, kuri atspindi srovės priklausomybę nuo įtampos ir varžos. Kitos dvi formulės, nors ir yra jos pasekmės, neturi fizinės prasmės.
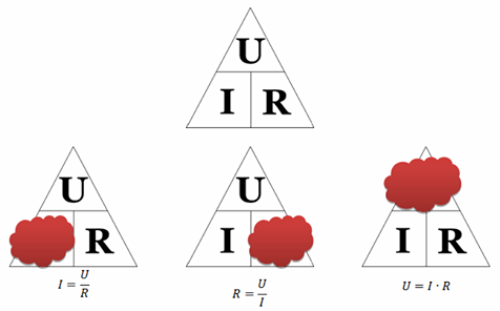
Skaičiavimai, atlikti naudojant Omo dėsnį grandinės atkarpai, bus teisingi, kai įtampa nurodyta voltais, varža – omais, o srovė – amperais. Jei naudojami keli šių dydžių vienetai (pvz., miliamperai, milivoltai, megohmai ir kt.), jie turi būti atitinkamai konvertuojami į amperus, voltus ir omas. Norėdami tai pabrėžti, Omo dėsnio formulė grandinės atkarpai kartais rašoma taip:
stiprintuvas = voltas / omas
Taip pat galite apskaičiuoti srovę miliamperais ir mikroamperais, o įtampa turėtų būti išreikšta voltais, o varža atitinkamai kiloomais ir megaomais.
Kiti straipsniai apie elektrą paprastai ir įperkamai:
Kas yra įtampa, srovė ir varža: kaip jie naudojami praktikoje
Kaip atsparumas priklauso nuo temperatūros
EML ir srovės šaltiniai: pagrindinės charakteristikos ir skirtumai
Elektrinis ir magnetinis laukas – koks skirtumas?
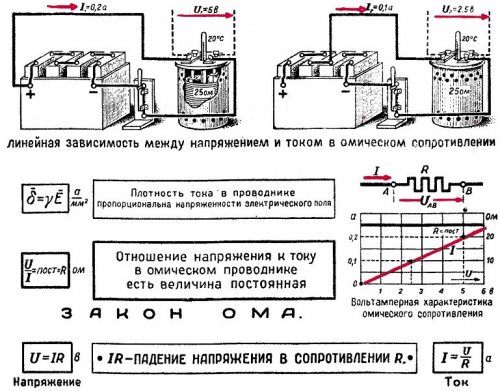
Omo dėsnis galioja kiekvienai grandinės atkarpai. Jei reikia nustatyti srovę tam tikroje grandinės atkarpoje, tai šioje atkarpoje veikiančią įtampą (1 pav.) reikia padalyti iš šios sekcijos varžos.
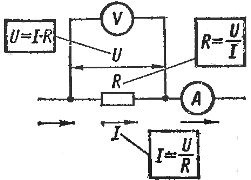
1 pav. Omo dėsnio taikymas grandinės atkarpai
Pateiksime pavyzdį, kaip apskaičiuoti srovę pagal Omo dėsnį... Tegul reikia nustatyti srovę lempoje, kurios varža 2,5 omo, jei į lempą tiekiama 5 V įtampa. 5 V padalijus iš 2,5 omų, gauname srovės vertę, lygią 2 A. Antrame pavyzdyje nustatome srovę, kuri tekės veikiama 500 V įtampos grandinėje, kurios varža yra 0,5 MΩ. Norėdami tai padaryti, išreiškiame pasipriešinimą omais. 500 V padalijus iš 500 000 omų, grandinėje randame srovę, kuri yra 0,001 A arba 1 mA.
Dažnai, žinant srovę ir varžą, įtampa nustatoma pagal Ohmo dėsnį. Parašykime formulę įtampai nustatyti
U = IR
Ši formulė rodo, kad tam tikros grandinės atkarpos galuose esanti įtampa yra tiesiogiai proporcinga srovei ir varžai... Šios priklausomybės prasmę suprasti nesunku.Jei grandinės sekcijos varža nesikeičia, srovę galima padidinti tik padidinus įtampą. Tai reiškia, kad esant pastoviai varžai, didesnė srovė atitinka didesnę įtampą. Jeigu reikia gauti vienodą srovę esant skirtingoms varžoms, tai esant didesnei varžai turi būti atitinkamai didesnė įtampa.
Įtampa grandinės atkarpoje dažnai vadinama įtampos kritimu... Tai dažnai sukelia nesusipratimų. Daugelis žmonių mano, kad įtampos kritimas yra tam tikra nereikalinga įtampa. Tiesą sakant, įtampos ir įtampos kritimo sąvokos yra lygiavertės. Nuostoliai ir įtampos kritimai – koks skirtumas?
Įtampos kritimas yra laipsniškas potencialo mažėjimas srovėje nešančioje grandinėje dėl to, kad grandinė turi aktyvią varžą. Pagal Omo dėsnį, įtampos kritimas kiekvienoje grandinės U atkarpoje lygus šios grandinės atkarpos R varžos sandaugai iš joje esančios srovės I, t.y. U – RI. Taigi, kuo didesnė grandinės atkarpos varža, tuo didesnis tam tikros srovės įtampos kritimas toje grandinės dalyje.
Omo įstatymo įtampos apskaičiavimas gali būti parodytas sekančiame pavyzdyje. Tegul 5 mA srovė praeina per grandinės atkarpą, kurios varža yra 10 kOhm, ir šioje atkarpoje būtina nustatyti įtampą.
Padauginus A = 0,005 A esant R — 10000 Ω, gauname įtampą, lygią 50 V. Tą patį rezultatą galima gauti 5 mA padauginus iš 10 kΩ: U = 50 in
Elektroniniuose prietaisuose srovė paprastai išreiškiama miliamperais, o varža – kiloomais.Todėl skaičiuojant pagal Ohmo dėsnį patogu naudoti būtent šiuos matavimo vienetus.
Omo dėsnis taip pat apskaičiuoja varžą, jei įtampa ir srovė yra žinomos. Šio atvejo formulė parašyta taip: R = U / I.
Atsparumas visada yra įtampos ir srovės santykis. Jei įtampa padidinama arba sumažinama kelis kartus, srovė padidės arba sumažės tiek pat kartų. Įtampos ir srovės santykis, lygus varžai, išlieka nepakitęs.
Atsparumo nustatymo formulė neturėtų būti suprantama taip, kad tam tikro laidininko varža priklauso nuo srovės ir įtampos. Žinoma, kad tai priklauso nuo laido ilgio, skerspjūvio ploto ir medžiagos. Išvaizda varžos nustatymo formulė primena srovės skaičiavimo formulę, tačiau tarp jų yra esminis skirtumas.
Srovė tam tikroje grandinės dalyje tikrai priklauso nuo įtampos ir varžos ir keičiasi jiems keičiantis. Ir šios grandinės atkarpos varža yra pastovi vertė, kuri nepriklauso nuo įtampos ir srovės pokyčių, bet yra lygi šių verčių santykiui.
Kai dviejose grandinės atkarpose teka ta pati srovė ir į jas tiekiamos skirtingos įtampos, akivaizdu, kad ta atkarpa, kuriai tiekiama didesnė įtampa, turi atitinkamai didesnę varžą.
Ir jei, veikiant tai pačiai įtampai, dviejose skirtingose grandinės dalyse teka skirtinga srovė, tada šioje sekcijoje visada bus mažesnė srovė, kuri turi didesnę varžą.Visa tai išplaukia iš pagrindinės Omo dėsnio formuluotės grandinės atkarpai, tai yra iš to, kad kuo didesnė srovė, tuo didesnė įtampa ir mažesnė varža.
Varžos apskaičiavimas naudojant Omo dėsnį grandinės atkarpai bus parodytas sekančiame pavyzdyje.Tegul reikia rasti atkarpos, per kurią teka 50 mA srovė, esant 40 V įtampai, varžą. amperais, gauname I = 0,05 A. Padalinkite 40 iš 0,05 ir sužinokite, kad varža yra 800 omų.
Omo dėsnį galima vizualizuoti vadinamosios srovės-įtampos charakteristikos pavidalu... Kaip žinia, tiesiogiai proporcingas ryšys tarp dviejų dydžių yra tiesė, einanti per pradžią. Ši priklausomybė paprastai vadinama linijine.
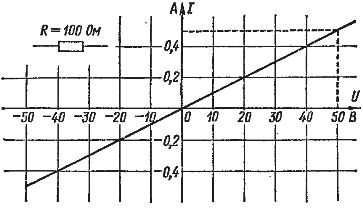
Fig. 2 parodytas kaip pavyzdinis Omo dėsnio grafikas grandinės atkarpai, kurios varža 100 omų. Horizontalioji ašis yra įtampa voltais, o vertikali ašis yra srovė amperais. Srovės ir įtampos skalę galima pasirinkti pagal pageidavimą. Nubrėžiama tiesi linija, kad kiekviename jos taške įtampos ir srovės santykis būtų 100 omų. Pavyzdžiui, jei U = 50 V, tai I = 0,5 A ir R = 50: 0,5 = 100 omų.
Ryžiai. 2… Omo dėsnis (srovės įtampos charakteristika)
Neigiamų srovės ir įtampos verčių Ohmo dėsnio grafikas yra toks pat. Tai reiškia, kad srovė grandinėje teka vienodai abiem kryptimis. Kuo didesnė varža, tuo mažesnė srovė gaunama esant tam tikrai įtampai ir tuo atidžiau juda tiesi linija.
Prietaisai, kuriuose srovės-įtampos charakteristika yra tiesė, einanti per pradinį tašką, tai yra varža išlieka pastovi, kai keičiasi įtampa ar srovė, vadinami tiesiniais įrenginiais... Taip pat vartojami terminai tiesinės grandinės, linijinės varžos.
Taip pat yra įrenginių, kurių varža keičiasi, kai keičiasi įtampa ar srovė. Tada srovės ir įtampos santykis išreiškiamas ne pagal Ohmo dėsnį, o sudėtingiau. Tokiems įtaisams srovės ir įtampos charakteristika nebus tiesi linija, einanti per pradinį tašką, o kreivė arba punktyrinė linija. Šie įrenginiai vadinami nelinijiniais.
Taip pat žiūrėkite šia tema: Omo dėsnio taikymas praktikoje