Elektrinis laukas, elektrostatinė indukcija, talpa ir kondensatoriai

Elektrinio lauko koncepcija

Yra žinoma, kad elektrinio lauko jėgos veikia erdvėje aplink elektros krūvius. Daugybė eksperimentų su įkrautais kūnais tai visiškai patvirtina. Erdvė aplink bet kurį įkrautą kūną yra elektrinis laukas, kuriame veikia elektrinės jėgos.

Lauko jėgų kryptis vadinama elektrinio lauko linijomis. Todėl visuotinai pripažįstama, kad elektrinis laukas yra jėgos linijų rinkinys.

Lauko linijos turi tam tikras savybes:

• jėgos linijos visada palieka teigiamą krūvį turintį kūną ir patenka į neigiamo krūvio kūną;

• jie išeina visomis kryptimis statmenai įkrauto kūno paviršiui ir įeina į jį statmenai;

• dviejų vienodai įkrautų kūnų jėgos linijos tarsi atstumia viena kitą, o priešingai įkrauti kūnai traukia.

Elektrinio lauko jėgos linijos visada yra atviros, kai jos nutrūksta įkrautų kūnų paviršiuje.Elektra įkrauti kūnai sąveikauja: priešingai įkrauti traukia ir panašiai atstumia.

Elektra įkrauti kūnai (dalelės), kurių krūviai q1 ir q2, sąveikauja vienas su kitu jėga F, kuri yra vektorinis dydis ir matuojamas niutonais (N). Kūnai su priešingais krūviais traukia vienas kitą, o su panašiais krūviais vienas kitą atstumia.

Pritraukimo arba atstūmimo jėga priklauso nuo kūnų krūvių dydžio ir atstumo tarp jų.

Įkrauti kūnai vadinami tašku, jei jų linijiniai matmenys yra maži, palyginti su atstumu r tarp kūnų. Jų sąveikos jėgos F dydis priklauso nuo krūvių q1 ir q2 dydžio, atstumo r tarp jų ir aplinkos, kurioje yra elektros krūviai.

Jei erdvėje tarp kūnų nėra oro, o koks nors kitas dielektrikas, tai yra nelaidus elektrai, tai kūnų sąveikos jėga sumažės.

Reikšmė, apibūdinanti dielektriko savybes ir parodanti, kiek kartų padidės sąveikos jėga tarp krūvių, jei duotas dielektrikas bus pakeistas oru, vadinama santykiniu tam tikro dielektriko laidumu.

Dielektrinė konstanta lygi: orui ir dujoms — 1; ebonitui — 2 — 4; žėručiui 5 — 8; aliejui 2 — 5; popieriui 2 — 2,5; parafinui — 2 — 2,6.

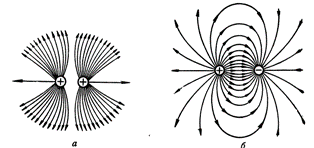
Dviejų įkrautų kūnų elektrostatinis laukas: a — talai įkraunami tuo pačiu pavadinimu, b — kūnai įkraunami skirtingai

Elektrostatinė indukcija

Jei laidžiam sferinės formos kūnui A, izoliuotam nuo aplinkinių objektų, suteikiamas neigiamas elektros krūvis, tai yra, kad jame būtų sukurtas elektronų perteklius, tada šis krūvis bus tolygiai paskirstytas kūno paviršiuje.Taip yra todėl, kad elektronai, atstumdami vienas kitą, linkę patekti į kūno paviršių.

Į kūno A lauką dedame neįkrautą kūną B, taip pat izoliuotą nuo aplinkinių objektų. Tada kūno B paviršiuje atsiras elektros krūviai, o kūno A šone – priešingas kūno A krūviui ( teigiamas ), o kitoje pusėje – krūvis, kurio pavadinimas toks pat, kaip ir kūno A krūvis (neigiamas). Taip pasiskirstę elektros krūviai lieka kūno B paviršiuje, kol jis yra kūno A lauke. Jei kūnas B pašalinamas iš lauko arba kūnas A pašalinamas, tai kūno B paviršiuje esantis elektros krūvis neutralizuojamas. Šis elektrifikavimo per atstumą būdas vadinamas elektrostatine indukcija arba elektrifikavimu veikiant.

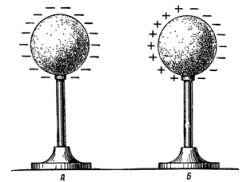
Elektrostatinės indukcijos reiškinys

Akivaizdu, kad tokią įelektrintą kūno būseną priverčia ir palaiko išskirtinai kūno A sukurto elektrinio lauko jėgos.

Jei tą patį darysime, kai kūnas A yra teigiamai įkrautas, tai laisvieji elektronai iš žmogaus rankos skubės į kūną B, neutralizuos teigiamą jo krūvį, o kūnas B bus neigiamai įkrautas.

Kuo didesnis kūno A elektrifikacijos laipsnis, t. y. kuo didesnis jo potencialas, tuo didesnį potencialą galima elektrifikuoti elektrostatinės indukcinės kūno B pagalba.

Taigi padarėme išvadą, kad elektrostatinės indukcijos reiškinys tam tikromis sąlygomis leidžia kaupti elektros ant laidžių kūnų paviršiaus.

Bet kuris kūnas gali būti įkrautas iki tam tikros ribos, tai yra iki tam tikro potencialo; potencialo padidėjimas už ribą sukelia kūno išmetimą į supančią atmosferą. Skirtingiems kūnams reikia skirtingų elektros energijos kiekių, kad jie įgytų tą patį potencialą. Kitaip tariant, skirtinguose kūnuose yra skirtingas elektros kiekis, tai yra, jie turi skirtingą elektrinį pajėgumą (arba tiesiog talpą).

Elektrinė talpa yra kūno gebėjimas išlaikyti tam tikrą elektros energijos kiekį, padidinant jo potencialą iki tam tikros vertės. Kuo didesnis kūno paviršiaus plotas, tuo daugiau elektros krūvio jis gali išlaikyti.

Jei kūnas yra rutulio formos, tada jo talpa yra tiesiogiai proporcinga rutulio spinduliui. Talpa matuojama faradais.

Farada – tai tokio kūno talpa, kuri, gavusi elektros krūvį pakabutyje, padidina savo potencialą vienu voltu... 1 faradas = 1 000 000 mikrofaradų.

Elektros inžinerijoje plačiai naudojama elektrinė talpa, tai yra laidžių kūnų savybė kaupti elektros krūvį savyje. Prietaisas pagrįstas šia savybe elektriniai kondensatoriai.

Kondensatoriaus talpa

Kondensatorius susideda iš dviejų metalinių plokščių (plokštelių), izoliuotų viena nuo kitos oro sluoksniu arba kitu dielektriku (žėručiu, popieriumi ir kt.).

Jei vienai iš plokščių yra suteiktas teigiamas krūvis, o kitai neigiamas, tai yra, įkraunamas jas priešingai, tada plokščių krūviai, vienas kitą traukiantys, bus laikomi ant plokštelių. Tai leidžia daug daugiau elektros energijos sutelkti ant plokštelių, nei tuo atveju, jei jos būtų įkraunamos per atstumą viena nuo kitos.

Todėl kondensatorius gali tarnauti kaip prietaisas, kuris savo plokštelėse kaupia nemažą elektros energijos kiekį. Kitaip tariant, kondensatorius yra elektros energijos kaupiklis.

Kondensatoriaus talpa yra lygi:

C = eS / 4pl

kur C yra talpa; e yra dielektriko dielektrinė konstanta; S – vienos plokštelės plotas cm2, NS – pastovus skaičius (pi), lygus 3,14; l — atstumas tarp plokščių cm.

Iš šios formulės matyti, kad didėjant plokščių plotui, didėja kondensatoriaus talpa, o didėjant atstumui tarp jų – mažėja.

Paaiškinkime šią priklausomybę. Kuo didesnis plokščių plotas, tuo daugiau elektros jos gali sugerti, todėl kondensatoriaus talpa bus didesnė.

Mažėjant atstumui tarp plokščių, didėja tarpusavio įtaka (indukcija) tarp jų krūvių, todėl galima sutelkti daugiau elektros energijos ant plokštelių ir dėl to padidinti kondensatoriaus talpą.

Taigi, jei norime gauti didelį kondensatorių, turime paimti didelio ploto plokštes ir jas izoliuoti plonu dielektriniu sluoksniu.

Formulė taip pat rodo, kad didėjant dielektriko dielektrinei konstantai, didėja ir kondensatoriaus talpa.

Todėl kondensatoriai, kurių geometriniai matmenys yra vienodi, bet turi skirtingus dielektrikus, turi skirtingą talpą.

Jei, pavyzdžiui, paimsime kondensatorių su oro dielektriku, kurio dielektrinė konstanta lygi vienetui, ir tarp jo plokščių įdėsime žėručio, kurio dielektrinė konstanta yra 5, tai kondensatoriaus talpa padidės 5 kartus.

Todėl tokios medžiagos kaip žėrutis, parafinu impregnuotas popierius ir kt., kurių dielektrinė konstanta yra daug didesnė nei oro, yra naudojamos kaip dielektrikai, norint gauti didelę talpą.

Atitinkamai išskiriami šie kondensatorių tipai: orinis, kietasis dielektrikas ir skystasis dielektrikas.

Kondensatoriaus įkrovimas ir iškrovimas. Poslinkio srovė

Į grandinę įtraukime pastovios talpos kondensatorių. Pastačius jungiklį ant kontakto a, kondensatorius bus įtrauktas į akumuliatoriaus grandinę. Miliampermetro adata tuo metu, kai kondensatorius yra prijungtas prie grandinės, nukryps ir taps nuliu.

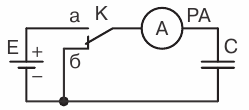
DC kondensatorius

Todėl elektros srovė praeidavo per grandinę tam tikra kryptimi. Jei jungiklis dabar yra ant kontakto b (ty uždarykite plokštes), miliampermetro adata pasisuks kita kryptimi ir grįš į nulį. Todėl srovė taip pat praėjo per grandinę, bet kita kryptimi. Išanalizuokime šį reiškinį.

Kai kondensatorius buvo prijungtas prie akumuliatoriaus, jis buvo įkrautas, tai yra, jo plokštės gavo vieną teigiamą, o kitą neigiamą krūvį. Atsiskaitymas tęsiasi iki potencialų skirtumą tarp kondensatoriaus plokščių nėra lygi akumuliatoriaus įtampai. Grandinėje nuosekliai sujungtas miliametras rodo kondensatoriaus įkrovimo srovę, kuri sustoja iškart po kondensatoriaus įkrovimo.

Atjungus kondensatorių nuo akumuliatoriaus jis liko įkrautas, o potencialų skirtumas tarp jo plokščių buvo lygus akumuliatoriaus įtampai.

Tačiau, kai tik kondensatorius buvo uždarytas, jis pradėjo išsikrauti ir iškrovimo srovė ėjo per grandinę, bet jau priešinga įkrovimo srovei kryptimi. Tai tęsiasi tol, kol išnyksta potencialų skirtumas tarp plokščių, tai yra, kol kondensatorius išsikrauna.

Todėl jei kondensatorius yra įtrauktas į nuolatinės srovės grandinę, srovė grandinėje tekės tik kondensatoriaus įkrovimo metu, o ateityje grandinėje nebus srovės, nes grandinę nutrauks dielektrikas. kondensatoriaus.

Štai kodėl jie sako, kad „kondensatorius nepraleidžia nuolatinės srovės“.

Elektros kiekis (Q), kurį galima sukoncentruoti ant kondensatoriaus plokštelių, jo talpa (C) ir į kondensatorių tiekiamos įtampos vertė (U) yra susiję su tokiu ryšiu: Q = CU.

Ši formulė rodo, kad kuo didesnė kondensatoriaus talpa, tuo daugiau elektros energijos galima sutelkti jame, nepadidinant jo plokščių įtampos.

Padidinus nuolatinės srovės talpos įtampą, padidėja ir kondensatoriaus sukauptos elektros energijos kiekis. Tačiau jei ant kondensatoriaus plokštelių bus prijungta didelė įtampa, kondensatorius gali būti „sulaužytas“, tai yra, veikiant šiai įtampai, dielektrikas kažkurioje vietoje subyrės ir leis per jį srovę. Tokiu atveju kondensatorius nustos veikti. Kad nebūtų pažeisti kondensatoriai, jie nurodo leistinos darbinės įtampos vertę.

Dielektrinės poliarizacijos reiškinys

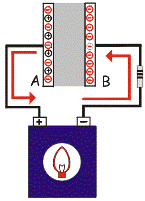Dabar panagrinėkime, kas vyksta dielektrike, kai kondensatorius įkraunamas ir iškraunamas, ir kodėl talpos vertė priklauso nuo dielektrinės konstantos?

Atsakymas į šį klausimą suteikia mums elektroninę materijos struktūros teoriją.

Dielektrike, kaip ir bet kuriame izoliatoriuje, laisvųjų elektronų nėra. Dielektriko atomuose elektronai yra tvirtai surišti su šerdimi, todėl kondensatoriaus plokštelėms įjungta įtampa nesukelia kryptingo elektronų judėjimo jo dielektrike, t.y. elektros srovė, kaip ir laidų atveju.

Tačiau veikiant elektrinio lauko jėgoms, kurias sukuria įkrautos plokštės, aplink atomo branduolį besisukantys elektronai pasislenka link teigiamai įkrautos kondensatoriaus plokštės. Tuo pačiu metu atomas ištemptas lauko linijų kryptimi.Tokia dielektrikų atomų būsena vadinama poliarizuota, o pats reiškinys – dielektrine poliarizacija.

Kai kondensatorius išsikrauna, dielektriko poliarizuota būsena nutrūksta, tai yra, dėl poliarizacijos dingsta elektronų poslinkis branduolio atžvilgiu ir atomai grįžta į įprastą nepoliarizuotą būseną. Nustatyta, kad dielektriko buvimas susilpnina lauką tarp kondensatoriaus plokščių.

Skirtingi dielektrikai, veikiami to paties elektrinio lauko, poliarizuojasi skirtingais laipsniais. Kuo lengviau dielektrikas poliarizuojamas, tuo labiau jis susilpnina lauką. Pavyzdžiui, oro poliarizacija sukelia mažiau lauko susilpnėjimo nei bet kurio kito dielektriko poliarizacija.

Tačiau lauko tarp kondensatoriaus plokščių susilpnėjimas leidžia sutelkti į jas didesnį elektros Q kiekį esant tokiai pačiai įtampai U, o tai savo ruožtu padidina kondensatoriaus talpą, nes C = Q / U .

Taigi padarėme išvadą - kuo didesnė dielektriko dielektrinė konstanta, tuo didesnė kondensatoriaus, kuriame yra šis dielektrikas, talpa.

Elektronų poslinkis dielektriko atomuose, vykstantis, kaip jau minėjome, veikiant elektrinio lauko jėgoms, dielektrike susidaro pirmuoju lauko veikimo momentu srovė vadinama nukreipimo srove... Ji taip pavadinta todėl, kad skirtingai nuo laidumo srovės metaliniuose laiduose, poslinkio srovė susidaro tik dėl jų atomuose judančių elektronų poslinkio.

Dėl šios poslinkio srovės kondensatorius, prijungtas prie kintamosios srovės šaltinio, tampa jo laidininku.

Taip pat žiūrėkite šia tema: Elektrinis ir magnetinis laukai: kokie yra skirtumai?

Pagrindinės elektrinio lauko charakteristikos ir pagrindinės terpės elektrinės charakteristikos (pagrindiniai terminai ir apibrėžimai)

Elektrinio lauko stiprumas

Vektorinis dydis, apibūdinantis elektrinio lauko jėgos poveikį elektra įkrautiems kūnams ir dalelėms, lygus jėgos, kuria elektrinis laukas veikia nejudantį taškinio krūvio kūną, įvestą nagrinėjamame lauko taške, santykio ribai. šio kūno krūvis, kai šis krūvis linkęs į nulį ir kurio kryptis, kaip manoma, sutampa su jėgos, veikiančios teigiamai įkrautą taškinį kūną, kryptimi.

Elektrinio lauko linija

Tiesė bet kuriame taške, kurios liestinė sutampa su elektrinio lauko stiprumo vektoriaus kryptimi.

Elektrinė poliarizacija

Medžiagos būsena, kuriai būdinga tai, kad tam tikro tos medžiagos tūrio elektrinis momentas turi kitokią reikšmę nei nulis.

Elektrinis laidumas

Medžiagos savybė, veikiant laikui bėgant nekintančiam elektriniam laukui, pravesti elektros srovę, kuri laikui bėgant nekinta.

Dielektrinis

Medžiaga, kurios pagrindinė elektrinė savybė yra gebėjimas poliarizuotis elektriniame lauke ir kurioje galimas ilgalaikis elektrostatinio lauko egzistavimas.

Laidi medžiaga

Medžiaga, kurios pagrindinė elektrinė savybė yra elektrinis laidumas.

direktorius

Laidus kūnas.

Puslaidininkinė medžiaga (puslaidininkis)

Medžiaga, kurios elektrinis laidumas yra tarpinis tarp laidžios medžiagos ir dielektriko ir kurios skiriamosios savybės yra: ryški elektros laidumo priklausomybė nuo temperatūros; elektros laidumo pokytis veikiant elektriniam laukui, šviesai ir kitiems išorės veiksniams; didelė jo elektrinio laidumo priklausomybė nuo įterptų priemaišų kiekio ir pobūdžio, o tai leidžia sustiprinti ir koreguoti elektros srovę, taip pat kai kurias energijos rūšis paversti elektra.

Poliarizacija (poliarizacijos intensyvumas)

Vektorinis dydis, apibūdinantis dielektriko elektrinės poliarizacijos laipsnį, lygus tam tikro dielektriko tūrio elektrinio momento santykio su šiuo tūriu ribai, kai pastarasis linkęs į nulį.

Elektrinė konstanta

Skaliarinis dydis, apibūdinantis elektrinį lauką ertmėje, lygus viso elektrinio krūvio, esančio tam tikrame uždarame paviršiuje, ir elektrinio lauko stiprumo vektoriaus srauto per šį paviršių tuštumoje santykiui.

Absoliutus dielektrinis jautrumas

Skaliarinis dydis, apibūdinantis dielektriko savybę būti poliarizuotam elektrinėje masėje, lygus poliarizacijos dydžio ir elektrinio lauko stiprio dydžio santykiui.

Dielektrinis jautrumas

Absoliutaus dielektrinio jautrumo nagrinėjamame dielektriko taške ir elektros konstantos santykis.

Elektrinis poslinkis

Vektorinis dydis, lygus elektrinio lauko stiprumo nagrinėjamame taške geometrinei sumai, padaugintai iš elektrinės konstantos ir poliarizacijos tame pačiame taške.

Absoliuti dielektrinė konstanta

Skaliarinis dydis, apibūdinantis dielektriko elektrines savybes ir lygus elektrinio poslinkio dydžio ir elektrinio lauko įtampos dydžio santykiui.

Dielektrinė konstanta

Absoliučios dielektrinės konstantos nagrinėjamame dielektriko taške ir elektrinės konstantos santykis.

Poslinkio elektros linija

Tiesė, kurios kiekviename taške jos liestinė sutampa su elektrinio poslinkio vektoriaus kryptimi.

Elektrostatinė indukcija

Elektros krūvių indukcijos ant laidžio kūno, veikiant išoriniam elektrostatiniam laukui, reiškinys.

Stacionarus elektrinis laukas

Laikui bėgant nekintančių elektros srovių elektrinis laukas, jei srovės laidininkai yra nejudantys.

Potencialus elektrinis laukas

Elektrinis laukas, kuriame elektrinio lauko stiprumo vektoriaus rotorius visur lygus nuliui.

Sūkurinis elektrinis laukas

Elektrinis laukas, kuriame intensyvumo vektoriaus rotorius ne visada lygus nuliui.

Elektrinių potencialų skirtumas dviejuose taškuose

Skaliarinis dydis, apibūdinantis potencialų elektrinį lauką, lygus šio lauko jėgų darbo santykio ribai, kai teigiamai įkrautas taškinis kūnas perkeliamas iš vieno lauko taško į kitą, į šio kūno krūvį. , kai kūno krūvis linkęs į nulį (kitaip: lygus elektrinio lauko stiprio tiesiniam integralui iš vieno duoto taško į kitą).

Elektrinis potencialas tam tikrame taške

Skirtumas tarp tam tikro taško ir kito nurodyto, bet savavališkai pasirinkto taško elektrinių potencialų.

Vieno laidininko elektrinė talpa

Skaliarinis dydis, apibūdinantis laidininko gebėjimą kaupti elektros krūvį, lygus laidininko krūvio ir jo potencialo santykiui, darant prielaidą, kad visi kiti laidininkai yra be galo nutolę ir kad be galo nutolusio taško potencialas yra lygus nuliui.

Elektrinė talpa tarp dviejų atskirų laidininkų

Skaliarinė vertė, lygi vieno laidininko elektros krūvio ir dviejų laidininkų elektrinių potencialų skirtumo santykio absoliučiai vertei, su sąlyga, kad šie laidininkai yra vienodo dydžio, bet priešingo ženklo ir kad visi kiti laidininkai yra be galo nutolę.

Kondensatorius

Dviejų laidininkų (plokštelių), atskirtų dielektriku, sistema, skirta panaudoti dviejų laidininkų talpą.

Kondensatoriaus talpa

Absoliuti vienos iš kondensatoriaus plokščių elektros krūvio ir potencialų skirtumo tarp jų santykio vertė, jei plokštės turi tokio paties dydžio ir priešingo ženklo krūvius.

Talpa tarp dviejų laidų laidų sistemoje (dalinė talpa)

Vieno iš laidininkų, įtrauktų į laidininkų sistemą, elektros krūvio santykio su potencialų skirtumu tarp jo ir kito laidininko absoliuti vertė, jei visi laidininkai, išskyrus pastarąjį, turi vienodą potencialą; jei įžeminimas yra įtrauktas į nagrinėjamą laidų sistemą, tada jo potencialas laikomas nuliu.

Trečiosios šalies elektrinis laukas

Šiluminių procesų, cheminių reakcijų, kontaktinių reiškinių, mechaninių jėgų ir kitų neelektromagnetinių (makroskopinio tyrimo metu) procesų sukeltas laukas; pasižymi stipriu poveikiu įkrautoms dalelėms ir kūnams, esantiems toje vietoje, kur egzistuoja šis laukas.

Indukuotas elektrinis laukas

Laike kintančio magnetinio lauko sukeltas elektrinis laukas.

Elektrovaros jėga E.d.S.

Skaliarinis dydis, apibūdinantis išorinio ir indukuoto elektrinio lauko gebėjimą indukuoti elektros srovę, lygią išorinio ir indukuoto elektrinio lauko stiprio tiesiniam integralui tarp dviejų taškų nagrinėjamu keliu arba išilgai nagrinėjamos uždaros grandinės.

Įtampa

Skaliarinis dydis, lygus susidarančio elektrinio lauko (elektrostatinio, stacionaraus, išorinio, indukcinio) stiprio tiesiniam integralui tarp dviejų nagrinėjamo kelio taškų.