Impulsinė srovė

Įvairiuose elektroniniuose įrenginiuose, pavyzdžiui, elektroninėje ir puslaidininkinėje įrangoje, tai yra stiprintuvuose, lygintuvuose, radijo imtuvuose, generatoriuose, televizoriuose, taip pat anglies mikrofonuose, telegrafuose ir daugelyje kitų prietaisų, jie plačiai naudojami pulsacinės srovės ir įtampos... nekartoti samprotavimų du kartus, kalbėsime tik apie sroves, bet viskas, kas susiję su srovėmis, galioja ir įtampoms.

Pulsuojančios srovės, kurios turi pastovią kryptį, bet keičia savo vertę, gali būti skirtingos. Kartais dabartinė reikšmė keičiasi iš didžiausios į mažiausią nenulinę vertę. Kitais atvejais srovė sumažinama iki nulio. Jeigu nuolatinės srovės grandinė nutrūksta tam tikru dažniu, tada tam tikrus laiko intervalus grandinėje nėra srovės.

Fig. 1 pavaizduoti įvairių bangų srovių grafikai. Fig. 1, a, b, srovių pokytis vyksta pagal sinusoidinė kreivė, tačiau šios srovės neturėtų būti laikomos sinusoidinėmis kintamosiomis srovėmis, nes srovės kryptis (ženklas) nekinta. Fig.1, c rodoma srovė, susidedanti iš atskirų impulsų, tai yra trumpalaikių srovės „smūgių“, atskirtų vienas nuo kito ilgesnės ar mažesnės trukmės pauzėmis, ir dažnai vadinama impulsine srove. Įvairios impulsinės srovės skiriasi viena nuo kitos impulsų forma ir trukme, taip pat pasikartojimo dažniu.

Bet kokios rūšies pulsuojančią srovę patogu laikyti dviejų srovių - tiesioginės ir kintamos, vadinamų termininėmis arba komponentinėmis srovėmis, suma. Bet kuri pulsuojanti srovė turi nuolatinės ir kintamosios srovės komponentus. Daugeliui tai atrodo keista. Tiesą sakant, pulsuojanti srovė yra srovė, kuri visą laiką teka viena kryptimi ir keičia savo vertę.

Kaip galite pasakyti, kad jame yra kintamoji srovė, kuri keičia kryptį? Tačiau jei per tą patį laidą vienu metu praeina dvi srovės – tiesioginė ir kintamoji, tai paaiškėja, kad tuo laidu tekės pulsuojanti srovė (2 pav.). Tokiu atveju kintamosios srovės amplitudė neturėtų viršyti nuolatinės srovės vertės. Tiesioginė ir kintamoji srovė negali tekėti atskirai per laidą. Jie prisideda prie bendro elektronų srauto, turinčio visas pulsuojančios srovės savybes.

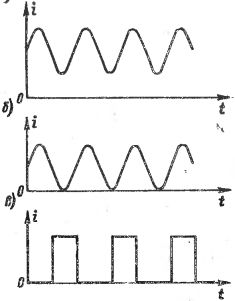
Ryžiai. 1. Įvairių bangų srovių grafikai

Kintamosios ir nuolatinės srovės srovių pridėjimas gali būti parodytas grafiškai. Fig. 2 parodyta nuolatinės srovės, lygios 15 mA, ir kintamosios srovės, kurios amplitudė yra 10 mA, grafikai. Jei susumuojame šių srovių reikšmes atskiriems laiko taškams, atsižvelgiant į srovių kryptis (ženklus), gauname bangos srovės grafiką, parodytą fig. 2 su paryškinta linija. Ši srovė svyruoja nuo žemiausios 5 mA iki didžiausios 25 mA.

Apsvarstytas srovių pridėjimas patvirtina pulsuojančios srovės kaip nuolatinių ir kintamųjų srovių sumos pagrįstumą. Šio vaizdavimo teisingumą patvirtina ir tai, kad kai kurių prietaisų pagalba galima atskirti šios srovės komponentus vieną nuo kito.

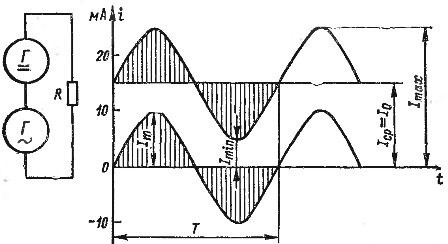
Ryžiai. 2. Pulsuojančios srovės gavimas pridedant nuolatinę ir kintamąją srovę.

Reikėtų pabrėžti, kad bet kokia srovė visada gali būti pavaizduota kaip kelių srovių suma. Pavyzdžiui, 5 A srovę galima laikyti viena kryptimi tekančių srovių 2 ir 3 A suma arba skirtingomis kryptimis tekančių srovių 8 ir 3 A suma, tai yra, kitaip tariant, srovių 8 skirtumu. ir 3 A. Nesunku rasti kitų dviejų ar daugiau srovių derinių, iš viso duodančių 5 A.

Čia yra visiškas panašumas su jėgų pridėjimo ir skaidymo principu. Jei bet kurį objektą veikia dvi vienodai nukreiptos jėgos, jas galima pakeisti viena bendra jėga. Priešingomis kryptimis veikiančios jėgos gali būti pakeistos vienetiniu skirtumu. Ir atvirkščiai, tam tikra jėga visada gali būti laikoma atitinkamų vienodai nukreiptų jėgų suma arba skirtumu tarp priešingos krypties jėgų.

Nebūtina skaidyti tiesioginių ar sinusinių kintamųjų srovių į komponentines sroves. Jeigu pulsuojančią srovę pakeisime nuolatinių ir kintamų srovių suma, tai šioms komponentinėms srovėms pritaikius žinomus nuolatinės ir kintamosios srovės dėsnius, galima išspręsti daugybę problemų ir atlikti reikiamus skaičiavimus, susijusius su pulsuojančia srove.

Pulsuojančios srovės, kaip nuolatinių ir kintamųjų srovių sumos, samprata yra sutartinė.Žinoma, negalima daryti prielaidos, kad tam tikrais laiko intervalais nuolatinė ir kintamoji srovė tikrai teka viena link kitos išilgai laido. Tiesą sakant, nėra dviejų priešingų elektronų srautų.

Tiesą sakant, pulsuojanti srovė yra viena srovė, kuri laikui bėgant keičia savo vertę. Teisingiau sakyti, kad pulsuojanti įtampa arba pulsuojantis EMF gali būti pavaizduotas kaip pastovių ir kintamų komponentų suma.

Pavyzdžiui, Fig. 2 parodyta, kaip algebriškai vieno generatoriaus konstanta emf pridedama prie kito generatoriaus kintamojo emf. Dėl to mes turime pulsuojantį EML, kuris sukelia atitinkamą pulsuojančią srovę. Tačiau sąlyginai galima laikyti, kad nuolatinis EMF grandinėje sukuria nuolatinę srovę, o kintamasis - kintamąją srovę, kurią sumuojant susidaro pulsuojanti srovė.

Kiekvieną pulsuojančią srovę galima apibūdinti didžiausiomis ir mažiausiomis Itax ir Itin reikšmėmis, taip pat jos pastoviais ir kintamaisiais komponentais. Pastovioji dedamoji žymima I0. Jei kintamoji dedamoji yra sinusoidinė srovė, tai jos amplitudė žymima It (visi šie dydžiai parodyti 2 pav.).

Jo nereikėtų painioti su It ir Itax. Be to, didžiausia srovės bangos Imax reikšmė neturėtų būti vadinama amplitude. Terminas amplitudė paprastai reiškia tik kintamąsias sroves. Kalbant apie pulsuojančią srovę, galime kalbėti tik apie jos kintamo komponento amplitudę.

Nuolatinė pulsuojančios srovės dedamoji gali būti vadinama jos vidutine verte Iav, tai yra aritmetine vidutine verte. Iš tiesų, jei atsižvelgsime į vieno pulsuojančios srovės periodo pokyčius, parodytus Fig.2, aiškiai matoma: pirmoje ciklo pusėje prie 15 mA srovės pridedama keletas reikšmių, keičiant srovės komponentą, kintančią nuo 0 iki 10 mA ir atgal iki 0, o antroje pusėje -ciklas, lygiai tos pačios srovės vertės atimamos iš srovės 15 mA.

Todėl 15 mA srovė iš tikrųjų yra vidutinė vertė. Kadangi srovė yra elektros krūvių perdavimas per laido skerspjūvį, tai Iav yra tokios nuolatinės srovės vertė, kuri per vieną periodą (arba visą periodų skaičių) neša tiek pat elektros energijos, kiek ši pulsuojanti srovė .

Sinusinės kintamos srovės atveju Iav vertė per periodą lygi nuliui, nes elektros kiekis, praėjęs per laidininko skerspjūvį per vieną pusę periodo, yra lygus elektros kiekiui, praeinančiam priešinga kryptimi per kitą pusę periodo. Srovių grafikuose, rodančiuose srovės i priklausomybę nuo laiko t, srovės nešamos elektros energijos kiekis išreiškiamas figūros plotu, kurį riboja srovės kreivė, nes elektros kiekis nustatomas pagal produktas, kad jis .

Sinusoidinei srovei teigiamų ir neigiamų pusbangių plotai lygūs.Pulsuojančioje srovėje, parodytoje pav. 2, pirmąjį pusmetį kintamosios srovės komponento pernešamos elektros energijos kiekis pridedamas prie srovės Iav pernešamos elektros energijos kiekio (paveikslėlyje tamsintas plotas). O per antrąjį ciklo pusmetį išimama lygiai tiek pat elektros energijos. Dėl to per visą laikotarpį perduodamas toks pat elektros energijos kiekis, kaip ir naudojant vieną nuolatinę srovę Iav, tai yra, stačiakampio Iav T plotas yra lygus plotui, kurį riboja bangos srovės kreivė.

Taigi pastovioji dedamoji arba vidutinė srovės vertė nustatoma perduodant elektros krūvius per laido skerspjūvį.

Dabartinė lygtis, parodyta fig. 2, be abejo, turėtų būti parašytas tokia forma:

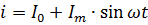
Pulsuojančios srovės galia turi būti apskaičiuojama kaip jos komponentų srovių galių suma. Pavyzdžiui, jei srovė, parodyta fig. 2, praeina per varžos R rezistorių, tada jo galia yra

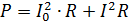
čia I = 0.7Im yra kintamojo komponento efektinė vertė.

Galite pristatyti bangos srovės Id efektinės vertės sąvoką. Galia apskaičiuojama įprastu būdu:

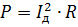
Prilyginę šią išraišką ankstesnei ir sumažinę ją su R, gauname:

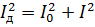
Tokius pačius santykius galima gauti ir esant stresui.