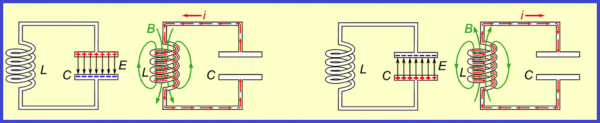
Elektromagnetinės vibracijos – be slopinimo ir priverstinės vibracijos

Elektromagnetiniai virpesiai grandinėje, susidedančioje iš induktoriaus ir kondensatoriaus, atsiranda dėl periodinio elektros energijos pavertimo magnetine energija ir atvirkščiai. Tokiu atveju periodiškai keičiasi kondensatoriaus plokščių elektros krūvis ir srovės dydis per ritę.

Elektromagnetinės vibracijos yra laisvos ir priverstinės. Laisvieji svyravimai, kaip taisyklė, yra slopinami dėl nenulinio kilpos pasipriešinimo, o priverstiniai virpesiai dažniausiai yra savaiminiai svyravimai.

Įsigyti vibracinėje grandinėje laisvųjų virpesių, pirmiausia turime išvesti šią sistemą iš pusiausvyros: informuoti kondensatorių su pradiniu įkrovimu q0 arba kaip nors inicijuoti srovės impulsą I0 per ritę.

Tai pasitarnaus kaip savotiškas impulsas ir grandinėje atsiras laisvi elektromagnetiniai virpesiai – prasidės kintamo kondensatoriaus įkrovimo ir iškrovimo per indukcinę ritę procesas ir atitinkamai kintamas ritės magnetinio lauko kilimas ir kritimas.

Virpesiai, kuriuos grandinėje palaiko išorinė kintamoji elektrovaros jėga, vadinami priverstiniais svyravimais. Taigi, kaip jau supratote, paprasčiausios virpesių sistemos, kurioje galima stebėti laisvus elektromagnetinius virpesius, pavyzdys yra virpesių grandinė, susidedanti iš C elektrinės talpos kondensatoriaus ir L induktyvumo ritės.

Tikroje virpesių grandinėje kondensatoriaus įkrovimo procesas periodiškai kartojamas, tačiau svyravimai greitai išnyksta, nes energija išsklaidoma daugiausia ant ritės laido aktyvios varžos R.

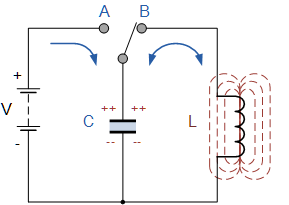
Apsvarstykite grandinę su idealia svyruojančia grandine. Pirmiausia įkraukime kondensatorių iš baterijos — duosime jam pradinį įkrovimą q0, tai yra, užpildysime kondensatorių energija. Tai bus maksimali kondensatoriaus We energija.

Kitas žingsnis yra atjungti kondensatorių nuo akumuliatoriaus ir prijungti jį lygiagrečiai su induktoriumi. Šiuo metu kondensatorius pradės išsikrauti, o ritės grandinėje atsiras didėjanti srovė. Kuo ilgiau kondensatorius išsikrauna, tuo daugiau įkrovos iš jo palaipsniui pereina į ritę, tuo didesnė srovė ritėje, todėl ritė kaupia energiją magnetinio lauko pavidalu.

Šis procesas nevyksta akimirksniu, o palaipsniui, nes ritė turi induktyvumą, o tai reiškia, kad atsiranda savaiminės indukcijos reiškinys, kuris susideda iš to, kad ritė vis tiek priešinasi srovės padidėjimui. Tam tikru momentu ritės magnetinio lauko energija pasiekia didžiausią įmanomą reikšmę Wm (priklausomai nuo to, kiek įkrovos pradžioje buvo perkelta į kondensatorių ir kokia grandinės varža).

Taip pat dėl ​​savaiminės indukcijos reiškinio srovė per ritę palaikoma ta pačia kryptimi, tačiau jos dydis mažėja ir elektros krūvis ilgainiui vėl kaupiasi kondensatoriuje. Tokiu būdu kondensatorius įkraunamas. Dabar jo plokštės turi priešingus įkrovimo ženklus nei eksperimento pradžioje, kai prijungėme kondensatorių prie akumuliatoriaus.

Kondensatoriaus energija pasiekė didžiausią įmanomą šios grandinės vertę. Srovė grandinėje sustojo. Dabar procesas pradeda eiti priešinga kryptimi.Ir tai tęsis vėl ir vėl, tai yra, bus laisvi elektromagnetiniai virpesiai.

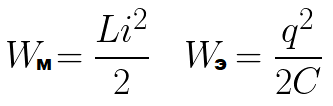
Jei grandinės R aktyvioji varža lygi nuliui, tai įtampa per kondensatoriaus plokštes ir srovė per ritę be galo svyruos pagal harmonikos dėsnį – kosinusą arba sinusą. Tai vadinama harmonine vibracija. Kondensatoriaus plokščių įkrova taip pat pasikeistų pagal harmonikos dėsnį.

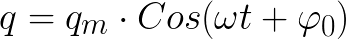
Idealiame cikle nuostolių nėra. O jei būtų, tai laisvųjų svyravimų grandinėje periodas priklausytų tik nuo kondensatoriaus talpos C ir ritės induktyvumo L. Šį laikotarpį galima rasti (idealiai ciklai, kai R = 0) naudojant Tomsono formulę:

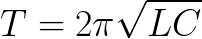
Atitinkamas dažnis ir ciklo dažnis randamas idealiai be nuostolių grandinei naudojant šias formules:

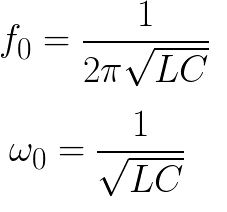
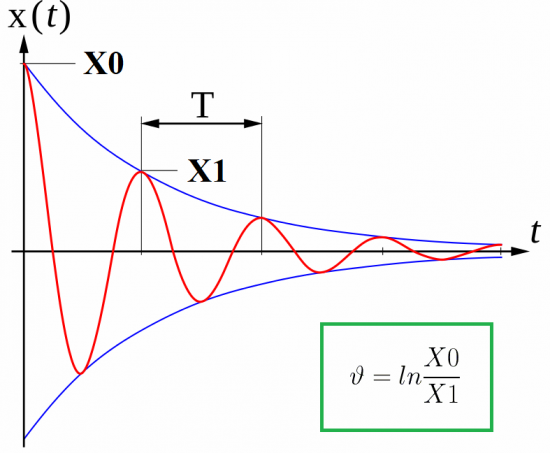
Tačiau idealių grandinių nėra, o elektromagnetiniai svyravimai yra slopinami dėl nuostolių dėl laidų šildymo. Priklausomai nuo grandinės varžos R vertės, kiekviena paskesnė maksimali kondensatoriaus įtampa bus mažesnė nei ankstesnė.

Ryšium su šiuo reiškiniu fizikoje įvedamas toks parametras kaip logaritminis virpesių mažėjimas arba slopinimo mažėjimas. Jis randamas kaip dviejų iš eilės einančių svyravimų maksimumų (to paties ženklo) santykio natūralusis logaritmas:

Logaritminis virpesių sumažinimas yra susijęs su idealiu svyravimo periodu tokiu ryšiu, kur galima įvesti papildomą parametrą, vadinamąjį. Slopinimo koeficientas:

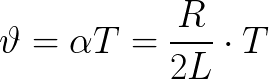
Slopinimas turi įtakos laisvųjų virpesių dažniui. Todėl formulė, leidžianti rasti laisvųjų slopintų virpesių dažnį tikroje svyruojančioje grandinėje, skiriasi nuo idealios grandinės formulės (atsižvelgiama į slopinimo koeficientą):

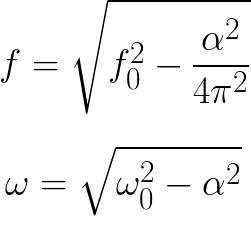
Sudaryti svyravimus grandinėje išjungtas, šiuos nuostolius būtina papildyti ir kompensuoti kas pusę laikotarpio. Tai pasiekiama nuolatinių virpesių generatoriuose, kur išorinis EML šaltinis šilumos nuostolius kompensuoja savo energija. Tokia svyravimų sistema su išoriniu EML šaltiniu vadinama savaime svyruojančia.