Aktyvioji ir reaktyvioji varža, varžos trikampis

Aktyvumas ir reaktyvumas

Varža, kurią suteikia leidimai ir vartotojai nuolatinės srovės grandinėse, vadinama omine varža.

Jei bet kuris laidas yra įtrauktas į kintamosios srovės grandinę, paaiškėja, kad jo varža bus šiek tiek didesnė nei nuolatinės srovės grandinėje. Taip yra dėl reiškinio, vadinamo odos efektu (paviršiaus efektas).

Jo esmė yra tokia. Kai laidu teka kintamoji srovė, jo viduje egzistuoja kintamasis magnetinis laukas, kertantis laidą. Šio lauko magnetinės jėgos linijos laidininke sukelia EML, tačiau skirtinguose laidininko skerspjūvio taškuose jis nebus vienodas: labiau link skerspjūvio centro ir mažiau į periferiją.

Taip yra dėl to, kad taškus, esančius arčiau centro, kerta daugybė jėgos linijų. Veikiant šiam EMF, kintamoji srovė nebus paskirstyta tolygiai visoje laidininko dalyje, bet arčiau jo paviršiaus.

Tai prilygsta naudingojo laidininko skerspjūvio sumažinimui ir dėl to jo atsparumo kintamajai srovei padidinimui. Pavyzdžiui, 1 km ilgio ir 4 mm skersmens varinė viela atlaiko: DC — 1,86 omo, AC 800 Hz — 1,87 omo, AC 10 000 Hz — 2,90 omo.

Atsparumas, kurį laidininkas suteikia kintamajai srovei, praeinančiam per jį, vadinama aktyvia varža.

Jei kuris nors vartotojas neturi induktyvumo ir talpos (kaitrinė lemputė, šildymo prietaisas), tai taip pat bus aktyvioji kintamosios srovės varža.

Aktyvioji varža – fizikinis dydis, apibūdinantis elektros grandinės (ar jos ploto) varžą elektros srovei dėl negrįžtamo elektros energijos virsmo kitomis formomis (daugiausia šiluma). Išreiškiamas omais.

Aktyvus pasipriešinimas priklauso nuo AC dažnisdidėja su jo didėjimu.

Tačiau daugelis vartotojų turi indukcines ir talpines savybes, kai per juos teka kintamoji srovė. Šie vartotojai apima transformatorius, droselius, elektromagnetai, kondensatoriai, įvairių tipų laidai ir daugelis kitų.

Pravažiuojant pro juos kintamoji srovė būtina atsižvelgti ne tik į aktyvumą, bet ir į reaktyvumą dėl to, kad vartotojas turi indukcinių ir talpinių savybių.

Yra žinoma, kad jei nuolatinė srovė, einanti per kiekvieną ritę, yra nutraukta ir uždaryta, tuo pačiu metu, kai keičiasi srovė, pasikeis ir ritės viduje esantis magnetinis srautas, dėl kurio atsiras saviindukcijos EML. joje.

Tas pats bus stebimas ir ritėje, įtrauktoje į kintamosios srovės grandinę, su vieninteliu skirtumu, kad taškas nuolat kinta tiek pagal dydį, tiek į ir į. Todėl į ritę prasiskverbiančio magnetinio srauto dydis nuolat keisis ir sukels Saviindukcijos EMF.

Tačiau saviindukcijos emf kryptis visada yra tokia, kad ji prieštarauja srovės pokyčiams. Taigi, didėjant srovei ritėje, savaime sukeltas EML bus linkęs sulėtinti srovės didėjimą, o mažėjant srovei, atvirkščiai, ji bus linkusi palaikyti nykstančią srovę.

Iš to išplaukia, kad į kintamosios srovės grandinę įtrauktoje ritėje (laidyje) atsirandantis saviindukcijos EML visada veiks prieš srovę, sulėtindamas jos pokyčius. Kitaip tariant, savaiminės indukcijos EML gali būti laikomas papildoma varža, kuri kartu su aktyvia ritės varža neutralizuoja kintamąją srovę, praeinančią per ritę.

Varža, kurią emf siūlo kintamajai srovei savaiminės indukcijos būdu, vadinama indukcine varža.

Indukcinė varža bus tuo didesnė vartotojo (grandinės) induktyvumas ir didesnis kintamosios srovės dažnis. Ši varža išreiškiama formule xl = ωL, kur xl – indukcinė varža omais; L — induktyvumas henry (gn); ω — kampinis dažnis, kur f — srovės dažnis).

Be indukcinės varžos, yra ir talpa, dėl to, kad laidai ir ritės yra talpos, ir kai kuriais atvejais dėl kondensatorių įtraukimo į kintamosios srovės grandinę.Didėjant vartotojo (grandinės) talpai C ir srovės kampiniam dažniui, talpinė varža mažėja.

Talpinė varža lygi xc = 1 / ωC, kur xc – talpinė varža omais, ω – kampinis dažnis, C – vartotojo talpa faradais.

Daugiau apie tai skaitykite čia: Reaktyvumas elektrotechnikoje

Atsparumo trikampis

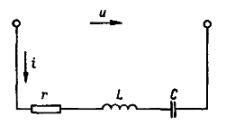
Apsvarstykite grandinę, kurios aktyviojo elemento varža r, induktyvumas L ir talpa C.

Ryžiai. 1. Kintamosios srovės grandinė su rezistoriumi, induktoriumi ir kondensatoriumi.

Tokios grandinės varža yra z = √r2+ (хl — xc)2) = √r2 + х2)

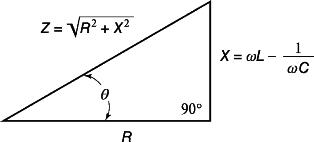
Grafiškai ši išraiška gali būti pavaizduota vadinamojo pasipriešinimo trikampio pavidalu.

Fig. 2. Atsparumo trikampis

Atsparumo trikampio hipotenuzė reiškia bendrą grandinės varžą, kojos - aktyviąją ir reaktyviąją varžą.

Jei viena iš grandinės varžų yra (aktyvioji arba reaktyvioji), pavyzdžiui, 10 ar daugiau kartų mažesnė už kitą, tada mažesnė gali būti nepaisoma, kurią galima lengvai patikrinti tiesioginiu skaičiavimu.