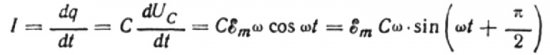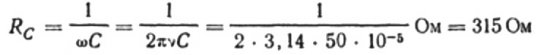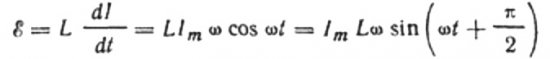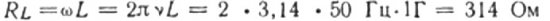Talpinė ir indukcinė varža kintamosios srovės grandinėje

Jei į nuolatinės srovės grandinę įtrauksime kondensatorių, pamatysime, kad jis turi begalinę varžą, nes nuolatinė srovė tiesiog negali praeiti pro dielektriką tarp plokščių, nes dielektrikas pagal apibrėžimą nelaidžia nuolatinės elektros srovės.

Kondensatorius nutraukia nuolatinės srovės grandinę. Bet jei tas pats kondensatorius dabar yra įtrauktas į kintamosios srovės grandinę, tada paaiškėja, kad jo kondensatorius visiškai nesugenda, jis tiesiog kinta ir kraunasi, tai yra, elektros krūvis juda, o srovė išorinėje grandinėje yra išlaikytas.

Remiantis Maksvelo teorija, šiuo atveju galime teigti, kad kintamoji laidumo srovė kondensatoriaus viduje vis dar yra uždaryta, tik šiuo atveju - poslinkio srove. Tai reiškia, kad kintamosios srovės grandinėje esantis kondensatorius veikia kaip baigtinės vertės varžos tipas. Šis pasipriešinimas vadinamas talpinis.

Praktika jau seniai įrodė, kad laidininku tekančios kintamosios srovės kiekis priklauso nuo to laidininko formos ir nuo jį supančios terpės magnetinių savybių.Tiesiu laidu srovė bus didžiausia, o jei tas pats laidas bus suvyniotas į ritę su dideliu apsisukimų skaičiumi, srovė bus mažesnė.

O jei į tą pačią ritę įvedama feromagnetinė šerdis, srovė dar labiau sumažės. Todėl laidas suteikia kintamąją srovę ne tik su omine (aktyvia) varža, bet ir papildoma varža, priklausomai nuo laido induktyvumo.Ši varža vadinama indukcinis.

Jo fizinė reikšmė yra ta, kad kintanti srovė tam tikro induktyvumo laidininke inicijuoja tame laidininke savaiminės indukcijos EML, kuri yra linkusi užkirsti kelią srovės pokyčiams, tai yra, linkusi sumažinti srovę. Tai prilygsta laido varžos padidinimui.

Talpa kintamosios srovės grandinėje

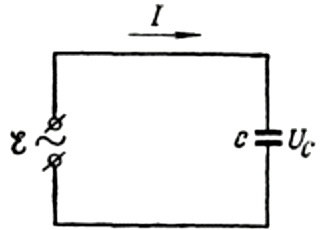
Pirma, pakalbėkime apie talpinę varžą išsamiau. Tarkime, kad C talpos kondensatorius yra prijungtas prie sinusinės kintamosios srovės šaltinio, tada šio šaltinio EML bus aprašyta tokia formule:

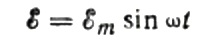
Mes nepaisysime įtampos kritimo jungiamuosiuose laiduose, nes paprastai jis yra labai mažas ir, jei reikia, gali būti svarstomas atskirai. Tarkime, kad kondensatoriaus plokščių įtampa yra lygi kintamosios srovės šaltinio įtampai. Tada:

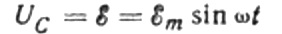
Bet kuriuo momentu kondensatoriaus įkrova priklauso nuo jo talpos ir įtampos tarp jo plokščių. Tada, atsižvelgiant į žinomą šaltinį, kuris buvo paminėtas aukščiau, gauname išraišką, kaip rasti kondensatoriaus plokščių įkrovą pagal šaltinio įtampą:

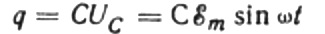
Tegul per be galo mažą laiką dt kondensatoriaus įkrova pasikeičia dq, tada srovė I tekės laidais nuo šaltinio iki kondensatoriaus, lygi:

Srovės amplitudės vertė bus lygi:

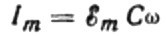
Tada paskutinė srovės išraiška bus tokia:

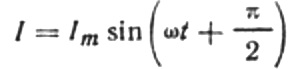
Perrašykime dabartinės amplitudės formulę taip:

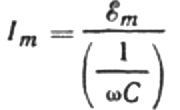
Šis santykis yra Ohmo dėsnis, kur kampinio dažnio ir talpos sandauga atlieka varžos vaidmenį ir iš tikrųjų yra išraiška, leidžianti rasti kondensatoriaus talpą sinusinės kintamosios srovės grandinėje:

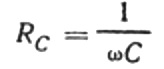
Tai reiškia, kad talpinė varža yra atvirkščiai proporcinga srovės kampiniam dažniui ir kondensatoriaus talpai. Nesunku suprasti fizinę šios priklausomybės prasmę.

Kuo didesnė kondensatoriaus talpa kintamosios srovės grandinėje ir kuo dažniau keičiasi srovės kryptis toje grandinėje, galiausiai daugiau bendro įkrovimo praeina per laiko vienetą per laidų, jungiančių kondensatorių su kintamosios srovės šaltiniu, skerspjūvį. Tai reiškia, kad srovė yra proporcinga talpos ir kampinio dažnio sandaugai.

Pavyzdžiui, apskaičiuokime kondensatoriaus, kurio elektrinė talpa 10 mikrofaradų, talpą sinusinės kintamosios srovės grandinei, kurios dažnis 50 Hz:

Jei dažnis būtų 5000 Hz, tada to paties kondensatoriaus varža būtų apie 3 omai.

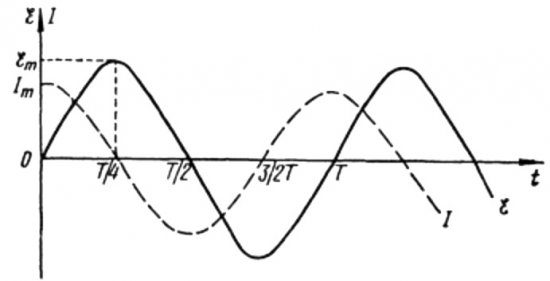
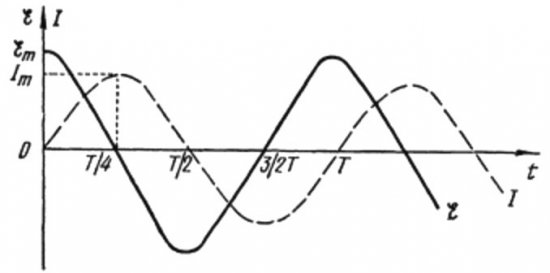
Iš aukščiau pateiktų formulių aišku, kad srovė ir įtampa kintamosios srovės grandinėje su kondensatoriumi visada keičiasi skirtingomis fazėmis. Srovės fazė nukreipia į įtampos fazę pi / 2 (90 laipsnių). Tai reiškia, kad maksimali srovė laike visada egzistuoja ketvirtadaliu anksčiau nei didžiausia įtampa. Taigi per talpinę varžą srovė nukreipia įtampą ketvirtadaliu laiko periodo arba 90 laipsnių faze.

Paaiškinkime fizinę šio reiškinio prasmę.Pirmą akimirką kondensatorius visiškai išsikrauna, todėl menkiausia įtampa, įjungta į jį, jau perkelia įkrovimus ant kondensatoriaus plokščių, sukurdama srovę.

Įkraunant kondensatorių, jo plokštelių įtampa didėja, tai užkerta kelią tolesniam įkrovos srautui, todėl srovė grandinėje mažėja, nepaisant to, kad plokštėms įtampa toliau didėja.

Tai reiškia, kad jei pradiniu momentu srovė buvo maksimali, tada, kai įtampa pasieks maksimalią po ketvirčio laikotarpio, srovė visiškai sustos.

Periodo pradžioje srovė yra maksimali, o įtampa – minimali ir pradeda didėti, tačiau po ketvirčio laikotarpio įtampa pasiekia maksimumą, tačiau srovė iki to laiko jau nukrito iki nulio. Taigi paaiškėja, kad įtampa lemia įtampą ketvirtadaliu periodo.

AC indukcinė varža

Dabar grįžkite prie indukcinio pasipriešinimo. Tarkime, kad per induktyvumo ritę teka kintamoji sinusoidinė srovė. Jis gali būti išreikštas taip:

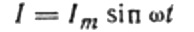
Srovė atsiranda dėl kintamos įtampos, tiekiamos į ritę. Tai reiškia, kad ant ritės atsiras saviindukcijos EML, kuri išreiškiama taip:

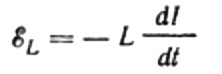
Vėlgi, mes nepaisome įtampos kritimo laiduose, jungiančiuose EMF šaltinį su ritė. Jų ominis atsparumas yra labai mažas.

Tegul kintamoji įtampa, tiekiama į ritę bet kuriuo momentu, yra visiškai subalansuota kylančios savaiminės indukcijos EML, kurios dydis yra lygus jai, bet priešinga kryptimi:

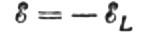
Tada mes turime teisę rašyti:

Kadangi į ritę tiekiamos įtampos amplitudė yra:

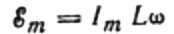
mes gauname:

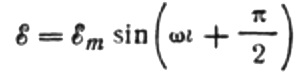
Didžiausią srovę išreikšime taip:

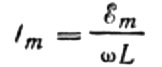
Ši išraiška iš esmės yra Ohmo dėsnis. Dydis, lygus induktyvumo ir kampinio dažnio sandaugai, čia vaidina pasipriešinimo vaidmenį ir yra ne kas kita, kaip indukcinė induktoriaus varža:

Taigi, indukcinė varža yra proporcinga ritės induktyvumui ir kintamosios srovės, einančios per tą ritę, kampiniam dažniui.

Taip yra dėl to, kad indukcinė varža atsiranda dėl savaiminio indukcijos EMF įtakos šaltinio įtampai, - savaiminės indukcijos EMF linkęs sumažinti srovę ir todėl grandinėje atneša varžą. Savaiminės indukcijos emf dydis, kaip žinoma, yra proporcingas ritės induktyvumui ir srovės per ją kitimo greičiui.

Pavyzdžiui, apskaičiuokime ritės, kurios induktyvumas yra 1 H, indukcinę varžą, kuri yra įtraukta į grandinę, kurios srovės dažnis yra 50 Hz:

Jei rutulio dažnis būtų 5000 Hz, tai tos pačios ritės varža būtų maždaug 31 400 omų.Prisiminkime, kad ritės laido ominė varža paprastai yra keli omai.

Iš aukščiau pateiktų formulių akivaizdu, kad srovės per ritę ir įtampos pokyčiai joje vyksta skirtingose ​​fazėse, o srovės fazė visada yra mažesnė už įtampos fazę esant pi / 2. Todėl maksimali srovė atsiranda ketvirtadaliu vėliau nei prasideda didžiausias įtempis.

Esant indukcinei varžai, srovė atsilieka nuo įtampos 90 laipsnių dėl savaime sukelto EML stabdymo efekto, kuris neleidžia srovei keistis (ir didėti, ir mažėti), todėl grandinėje su rite vėliau stebima maksimali srovė. nei maksimali įtampa.

Ritės ir kondensatoriaus kombinuotas veikimas

Jei ritę su kondensatoriumi prijungiate nuosekliai su kintamosios srovės grandine, tada ritės įtampa laikui bėgant padidins kondensatoriaus įtampą puse periodo, ty 180 laipsnių faze.

Talpinė ir indukcinė varža vadinama reagentai… Energija eikvojama ne reaktyviojoje varžoje, o aktyviojoje varžoje. Kondensatoriuje sukaupta energija periodiškai grąžinama atgal į šaltinį, kai kondensatoriuje išnyksta elektrinis laukas.

Lygiai taip pat ir su rite: kadangi ritės magnetinį lauką sukuria srovė, joje esanti energija per ketvirtį periodo kaupiasi, o kitą ketvirtį periodo grįžta į šaltinį. Šiame straipsnyje mes kalbėjome apie sinusinę kintamąją srovę, kuriai griežtai laikomasi šių taisyklių.

Kintamosios srovės sinusoidinėse grandinėse vadinami induktoriais su šerdimi dusinantistradiciškai naudojami srovės ribojimui. Jų pranašumas prieš reostatus yra tas, kad energija neišsisklaido dideliais kiekiais kaip šiluma.