Srovės ir įtampos RMS vertės

Kintamoji sinusoidinė srovė per laikotarpį turi skirtingas momentines vertes. Natūralu, kad kyla klausimas, kokia srovės vertė bus matuojama naudojant į grandinę įtrauktą ampermetrą?

Skaičiuojant kintamosios srovės grandines, taip pat atliekant elektrinius matavimus, nepatogu naudoti momentines arba amplitudines srovių ir įtampų vertes, o jų vidutinės vertės per tam tikrą laikotarpį yra lygios nuliui. Be to, periodiškai kintančios srovės elektrinis poveikis (išleidžiamos šilumos kiekis, tobulas veikimas ir kt.) negali būti įvertintas pagal šios srovės amplitudę.

Patogiausia buvo įvesti vadinamųjų efektyviųjų srovės ir įtampos verčių sąvokas... Šios sąvokos pagrįstos terminiu (arba mechaniniu) srovės veikimu, kuris nepriklauso nuo jos krypties.

Kintamosios srovės vidutinė kvadratinė vertė – tai nuolatinės srovės vertė, kuriai esant kintamos srovės laikotarpiu laidininke išsiskiria toks pat šilumos kiekis kaip ir kintamos srovės metu.

Įvertinti atliktus veiksmus kintamoji srovė, palyginsime jo veiksmus su nuolatinės srovės šiluminiu poveikiu.

Nuolatinės srovės galia P A, einanti per varžą r, bus P = P2r.

Kintamosios srovės galia išreiškiama kaip vidutinis momentinės galios Az2r poveikis per visą laikotarpį arba (I am x sinωT)2 NS r to paties laiko vidurkis.

Tegul vidutinė laikotarpio t2 reikšmė yra M. Prilyginę nuolatinės srovės galią ir kintamosios srovės galią, gauname: Az2r = Mr -n, iš kur Az = √M,

Dydis I vadinamas efektyvia kintamosios srovės verte.

Vidutinė i2 vertė esant kintamajai srovei nustatoma taip.

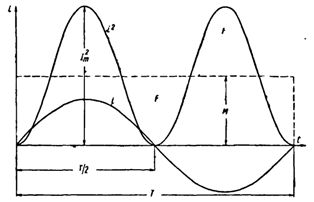
Sukonstruokime sinusoidinės srovės kreivę. Padalydami kiekvieną momentinę srovės vertę kvadratu, gauname P ir laiko kreivę.

AC efektinė vertė

Abi šios kreivės pusės yra virš horizontalios ašies, nes neigiamos srovės (-i) antroje periodo pusėje, pabrėžtos kvadratu, suteikia teigiamas vertes.

Sukurkite stačiakampį, kurio pagrindas T ir plotas lygus plotui, kurį riboja kreivė i2 ir horizontalioji ašis. Stačiakampio M aukštis atitiks vidutinę laikotarpio P reikšmę. Ši laikotarpio reikšmė, apskaičiuota naudojant aukštąją matematiką, bus lygi 1/2 I2m... Todėl M. = 1/2 I2m

Kadangi efektinė vertė Im kintamoji srovė yra Im = √M, tai galiausiai I = Im / √2

Panašiai ir įtampos U ir E vidutinių kvadratinių ir amplitudės verčių santykis yra toks:

U = Um / √2E = Em / √2

Aktyvios kintamųjų reikšmės žymimos didžiosiomis raidėmis be indeksų (I, U, E).

Remiantis tuo, kas išdėstyta aukščiau, galime teigti, kad kintamosios srovės efektyvioji vertė yra lygi tokiai nuolatinei srovei, kuri, eidama per tokią pat varžą kaip ir kintamoji, tuo pačiu metu išskiria tiek pat energijos.

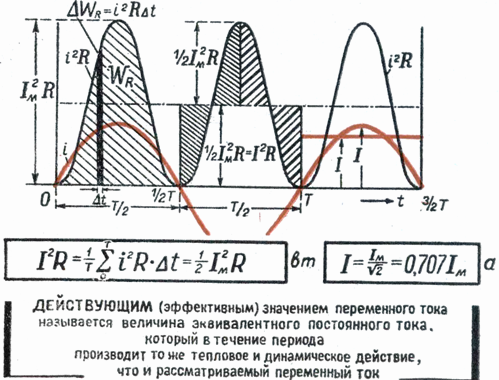
Į kintamosios srovės grandinę įtraukti elektros matavimo prietaisai (ampermetrai, voltmetrai) rodo efektyvias srovės ar įtampos vertes.

Kuriant vektorines diagramas, patogiau atidėti ne amplitudę, o efektyvias vektorių reikšmes. Tam vektorių ilgiai vieną kartą sumažinami √2. Tai nekeičia vektorių vietos diagramoje.