Elektrinio lauko charakteristikos

Straipsnyje aprašomos pagrindinės elektrinio lauko charakteristikos: potencialas, įtampa ir intensyvumas.

Kas yra elektrinis laukas

Norint sukurti elektrinį lauką, būtina sukurti elektros krūvį. Erdvės aplink krūvius (įkrautus kūnus) savybės skiriasi nuo erdvės, kurioje nėra krūvių, savybių. Tuo pačiu metu erdvės savybės, įvedant į ją elektros krūvį, akimirksniu nepasikeičia: pokytis prasideda nuo krūvio ir tam tikru greičiu plinta iš vieno erdvės taško į kitą.

Erdvėje, kurioje yra krūvis, pasireiškia mechaninės jėgos, veikiančios kitus į tą erdvę įvestus krūvius. Šios jėgos yra ne tiesioginio vieno krūvio poveikio kitam, o veikimo per kokybiškai pakeistą terpę rezultatas.

Erdvė aplink elektros krūvius, kurioje pasireiškia jėgos, veikiančios į ją įvestus elektros krūvius, vadinama elektriniu lauku.

Krūvis elektriniame lauke juda iš lauko pusės jį veikiančios jėgos kryptimi.Tokio krūvio ramybės būsena galima tik tada, kai krūviui veikia kokia nors išorinė (išorinė) jėga, kuri subalansuoja elektrinio lauko stiprumą.

Kai tik sutrinka pusiausvyra tarp išorinės jėgos ir lauko stiprumo, krūvis vėl pradeda judėti. Jo judėjimo kryptis visada sutampa su didesnės jėgos kryptimi.

Aiškumo dėlei elektrinis laukas dažniausiai vaizduojamas vadinamosiomis elektrinio lauko linijomis. Šios linijos sutampa su jėgų, veikiančių elektriniame lauke, kryptimi. Tuo pačiu buvo sutarta nubrėžti tiek linijų, kad jų skaičius kiekvienam 1 cm2 ploto, įrengto statmenai linijoms, būtų proporcingas lauko stiprumui atitinkamame taške.

Lauko kryptis paprastai laikoma lauko stiprumo, veikiančio teigiamą krūvį, esantį tam tikrame lauke, kryptis. Teigiamus krūvius atstumia teigiami krūviai ir traukia neigiami krūviai. Todėl laukas nukreipiamas iš teigiamų į neigiamus krūvius.

Jėgos linijų kryptis brėžiniuose nurodoma rodyklėmis. Mokslas įrodė, kad elektrinio lauko jėgos linijos turi pradžią ir pabaigą, tai yra, jos nėra savaime uždarytos. Remdamiesi numanoma lauko kryptimi, nustatome, kad jėgų linijos prasideda teigiamais krūviais (teigiamai įkrautais kūnais), o baigiasi neigiamais.

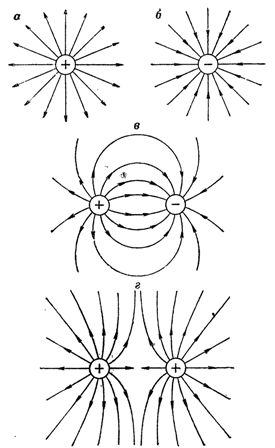
Ryžiai. 1. Elektrinio lauko atvaizdo, naudojant jėgos linijas, pavyzdžiai: a – elektrinis laukas su vienu teigiamu krūviu, b – elektrinis laukas su vienu neigiamu krūviu, c – dviejų priešingų krūvių elektrinis laukas, d – an dviejų panašių krūvių elektrinis laukas

Fig.1 pavaizduoti elektrinio lauko pavyzdžiai, pavaizduoti naudojant jėgos linijas. Reikia atsiminti, kad elektrinio lauko linijos yra tik būdas grafiškai pavaizduoti lauką. Čia nėra didesnės jėgos linijos sąvokos esmės.

Kulono dėsnis

Dviejų krūvių sąveikos stiprumas priklauso nuo krūvių dydžio ir tarpusavio išsidėstymo, taip pat nuo jų aplinkos fizinių savybių.

Dviejų elektrifikuotų fizinių kūnų, kurių matmenys yra nereikšmingi, palyginti su atstumu tarp kūnų, sąveikos gijimas nustatomas matematiškai taip:

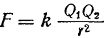
čia F – krūvių sąveikos jėga niutonais (N), k – atstumas tarp krūvių metrais (m), Q1 ir Q2 – elektros krūvių dydis kulonais (k), k – proporcingumo koeficientas, kurio reikšmė priklauso nuo krūvius supančios terpės savybių.

Aukščiau pateikta formulė skamba taip: dviejų taškinių krūvių sąveikos jėga yra tiesiogiai proporcinga šių krūvių dydžių sandaugai ir atvirkščiai proporcinga atstumo tarp jų kvadratui (Kulono dėsnis).

Norėdami nustatyti proporcingumo koeficientą k, naudokite išraišką k = 1 /(4πεεО).

Elektrinio lauko potencialas

Elektrinis laukas visada suteikia krūviui judėjimą, jei jį veikiančių lauko jėgų nesubalansuoja jokios išorinės jėgos. Tai reiškia, kad elektrinis laukas turi potencialią energiją, tai yra, gebėjimą atlikti darbą.

Perkeliant krūvį iš vieno erdvės taško į kitą, elektrinis laukas iš tiesų veikia, dėl to mažėja potencialios energijos tiekimas laukui.Jei krūvis juda elektriniame lauke, veikiant kokiai nors išorinei jėgai, veikiančiai priešingai lauko jėgoms, tai darbą atlieka ne elektrinio lauko jėgos, o išorinės jėgos. Tokiu atveju lauko potencinė energija ne tik nesumažėja, bet, priešingai, didėja.

Darbas, kurį atlieka išorinė jėga, judinanti krūvį elektriniame lauke, yra proporcinga tam judėjimui priešingų lauko jėgų dydžiui. Darbas, kurį šiuo atveju atlieka išorinės jėgos, yra visiškai išleidžiamas potencialiai lauko energijai padidinti. Norint apibūdinti lauką iš jo potencialios energijos pusės, vadinamas dydis, vadinamas elektrinio lauko potencialu.

Šio kiekio esmė yra tokia. Tarkime, kad teigiamas krūvis yra už nagrinėjamo elektrinio lauko ribų. Tai reiškia, kad laukas praktiškai neturi įtakos duotam krūviui. Tegul išorinė jėga įveda šį krūvį į elektrinį lauką ir, įveikusi pasipriešinimą judėjimui, kurį sukelia lauko jėgos, perkelia krūvį į tam tikrą lauko tašką. Jėgos atliktas darbas, taigi ir kiekis, kuriuo padidėjo lauko potencinė energija, visiškai priklauso nuo lauko savybių. Todėl šis darbas gali apibūdinti tam tikro elektrinio lauko energiją.

Elektrinio lauko energija, susijusi su teigiamo krūvio vienetu, esančiu tam tikrame lauko taške, vadinama lauko potencialu tam tikrame taške.

Jei potencialas žymimas raide φ, krūvis – raide q, o darbas, skirtas krūviui perkelti W, tada lauko potencialas tam tikrame taške bus išreikštas formule φ = W / q.

Iš to išplaukia, kad elektrinio lauko potencialas tam tikrame taške yra skaitiniu požiūriu lygus išorinės jėgos atliekamam darbui, kai vienetinis teigiamas krūvis juda iš lauko link tam tikro taško. Lauko potencialas matuojamas voltais (V). Jei perduodant vieną kuloną elektros energijos už lauko į tam tikrą tašką, išorinės jėgos atliko darbą, lygų vienam džauliui, tada potencialas tam tikrame lauko taške yra lygus vienam voltui: 1 voltas = 1 džaulis / 1 kulonas

Elektrinio lauko stiprumas

Bet kuriame elektriniame lauke teigiami krūviai juda iš didesnio potencialo taškų į mažesnio potencialo taškus. Priešingai, neigiami krūviai juda iš mažesnio potencialo taškų į didesnio potencialo taškus. Abiem atvejais darbas atliekamas potencialios elektrinio lauko energijos sąskaita.

Jei žinome šį darbą, tai yra, kiek sumažėjo lauko potencinė energija, kai teigiamas krūvis q juda iš lauko taško 1 į tašką 2, tada lengva rasti įtampą tarp šių lauko taškų. laukas U1,2:

U1,2 = A / q,

čia A yra lauko jėgų atliktas darbas, kai krūvis q perkeliamas iš taško 1 į tašką 2. Įtampa tarp dviejų elektrinio lauko taškų skaitine prasme yra lygi nuliui, perkeliant vienetinį teigiamą krūvį iš vieno taško lauke pas kitą.

Kaip matyti, įtampa tarp dviejų lauko taškų ir potencialų skirtumas tarp tų pačių taškų reiškia tą patį fizinį vienetą... Todėl terminai įtampa ir potencialų skirtumas yra vienodi. Įtampa matuojama voltais (V).

Įtampa tarp dviejų taškų yra lygi vienam voltui, jei perkeliant vieną kuloną elektros iš vieno lauko taško į kitą lauko jėgos veikia lygiai vienam džauliui: 1 voltas = 1 džaulis / 1 kulonas

Elektrinio lauko stiprumas

Iš Kulono dėsnio išplaukia, kad tam tikro krūvio, veikiančio kitą šiame lauke esantį krūvį, elektrinio lauko stipris nėra vienodas visuose lauko taškuose. Elektrinį lauką bet kuriame taške galima apibūdinti jėgos, kuria jis veikia vienetinį teigiamą krūvį, esantį tam tikrame taške, dydžiu.

Žinant šią reikšmę, galima nustatyti jėgą F, veikiančią kiekvieną krūvį Q. Galite parašyti, kad F = Q x E, kur F yra jėga, veikianti krūvį Q, esantį lauko taške elektrinio lauko, E yra jėga, veikianti vienetinį teigiamą krūvį, esantį tame pačiame lauko taške. Dydis E, skaičiais lygus jėgai, kurią patiria vienetinis teigiamas krūvis tam tikrame lauko taške, vadinamas elektrinio lauko stipriu.