Kondensatoriaus įkrovimas ir iškrovimas

Kondensatoriaus įkrovimas

Norėdami įkrauti kondensatorių, turite jį prijungti prie nuolatinės srovės grandinės. Fig. 1 parodyta kondensatoriaus įkrovimo grandinė. Kondensatorius C prijungtas prie generatoriaus gnybtų. Raktu galima uždaryti arba atidaryti grandinę. Išsamiai pažvelkime į kondensatoriaus įkrovimo procesą.

Generatorius turi vidinę varžą. Kai jungiklis uždarytas, kondensatorius įkraunamas iki įtampos tarp plokščių, lygių e. ir tt v. generatorius: Uc = E. Šiuo atveju plokštė, prijungta prie generatoriaus teigiamo gnybto, gauna teigiamą krūvį (+q), o antroji plokštė gauna vienodą neigiamą krūvį (-q). Krūvio dydis q yra tiesiogiai proporcingas kondensatoriaus C talpai ir jo plokščių įtampai: q = CUc

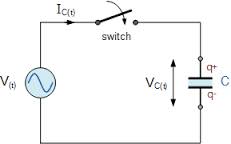
Pe. 1… Kondensatoriaus įkrovimo grandinė

Norint įkrauti kondensatoriaus plokštes, reikia, kad viena iš jų įgytų, o kita prarastų tam tikrą kiekį elektronų.Elektronų perkėlimas iš vienos plokštės į kitą vyksta išilgai išorinės grandinės, veikiant generatoriaus elektrovaros jėgai, o krūvių judėjimo grandinėje procesas yra ne kas kita, kaip elektros srovė, vadinama įkrovimo talpine srove A.

Įkrovimo srovė paprastai teka tūkstantosiomis sekundės dalimis, kol kondensatoriaus įtampa pasiekia vertę, lygią e. ir tt v. generatorius. Įtampos kilimo ant kondensatoriaus plokščių jo įkrovimo metu grafikas parodytas fig. 2, a, iš kurios matyti, kad įtampa Uc didėja tolygiai, iš pradžių sparčiai, o paskui vis lėčiau, kol tampa lygi e. ir tt v. generatorius E. Po to kondensatoriaus įtampa lieka nepakitusi.

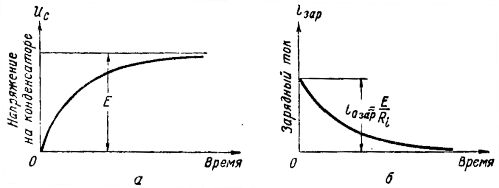
Ryžiai. 2. Įtampos ir srovės grafikai kraunant kondensatorių

Kai kondensatorius įkraunamas, per grandinę teka įkrovimo srovė. Įkrovimo srovės grafikas parodytas fig. 2, b. Pradiniu momentu įkrovimo srovė turi didžiausią vertę, nes įtampa kondensatoriuje vis dar lygi nuliui, o pagal Omo dėsnį iotax = E /Ri, nes visos e. ir kt. c generatorius taikomas varžai Ri.

Kai kondensatorius įkraunamas, tai yra, didėja įtampa jame, ji mažėja įkrovimo srovei. Kai kondensatoriuje jau yra įtampa, įtampos kritimas per varžą bus lygus skirtumui tarp e. ir tt v. generatoriaus ir kondensatoriaus įtampa, ty lygi E — U s. Todėl itax = (E-Us) / Ri

Iš čia matyti, kad didėjant Uc, ikraunasi, o esant Uc = E, įkrovimo srovė tampa lygi nuliui.

Daugiau apie Ohmo dėsnį skaitykite čia: Omo dėsnis grandinės atkarpai

Kondensatoriaus įkrovimo proceso trukmė priklauso nuo dviejų dydžių:

1) nuo generatoriaus Ri vidinės varžos,

2) nuo kondensatoriaus C talpos.

Fig. 2 pavaizduoti 10 mikrofaradų talpos kondensatoriaus elegantiškų srovių grafikai: 1 kreivė atitinka įkrovimo procesą iš generatoriaus su e. ir tt kai E = 100 V ir vidinė varža Ri = 10 omų, 2 kreivė atitinka įkrovimo procesą iš generatoriaus su ta pačia e. su, bet su mažesne vidine varža: Ri = 5 omai.

Palyginus šias kreives, matyti, kad esant mažesnei generatoriaus vidinei varžai, elegantiškos srovės stiprumas pradiniu momentu yra didesnis ir todėl įkrovimo procesas vyksta greičiau.

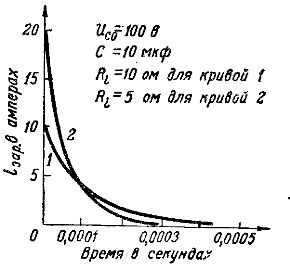
Ryžiai. 2. Įkrovimo srovių grafikai esant skirtingoms varžoms

Fig. 3 palyginami įkrovimo srovių grafikai kraunant iš to paties generatoriaus su e. ir tt kurių E = 100 V ir vidinė varža Ri= 10 omų dviejų skirtingos talpos kondensatorių: 10 mikrofaradų (1 kreivė) ir 20 mikrofaradų (2 kreivė).

Pradinė įkrovimo srovė iotax = E /Ri = 100/10 = 10 Abu kondensatoriai yra vienodi, kadangi didesnės talpos kondensatorius sukaupia daugiau elektros energijos, tuomet jo įkrovimo srovė turėtų užtrukti ilgiau, o įkrovimo procesas ilgesnis.

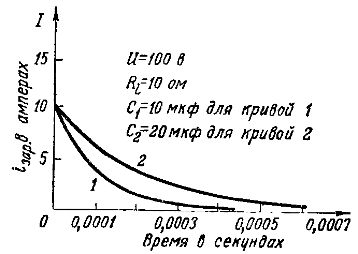
Ryžiai. 3. Skirtingos talpos įkrovimo srovių lentelės

Kondensatoriaus iškrova

Atjunkite įkrautą kondensatorių nuo generatoriaus ir pritvirtinkite varžą prie jo plokščių.

Kondensatoriaus Us plokštelėse yra įtampa, todėl uždaroje grandinėje tekės srovė, vadinama iškrovos talpinės srovės ires.

Srovė teka iš teigiamos kondensatoriaus plokštės per varžą į neigiamą plokštę. Tai atitinka elektronų pertekliaus perėjimą iš neigiamos plokštės į teigiamą, kur jų nėra.Eilučių kadrų procesas vyksta tol, kol dviejų plokščių potencialai yra lygūs, ty potencialų skirtumas tarp jų tampa lygus nuliui: Uc = 0.

Fig. 4a parodytas kondensatoriaus įtampos sumažėjimo grafikas iškrovimo metu nuo reikšmės Uco = 100 V iki nulio, o įtampa pirmiausia mažėja greitai, o vėliau lėčiau.

Fig. 4, b parodytas iškrovos srovės pokyčių grafikas. Iškrovos srovės stiprumas priklauso nuo varžos R vertės ir pagal Omo dėsnį ires = Uc/R

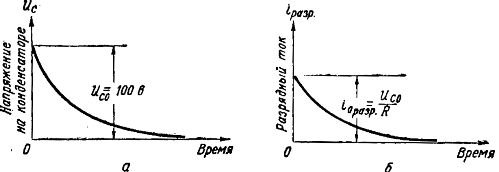
Ryžiai. 4. Įtampos ir srovių grafikai kondensatoriaus iškrovos metu

Pradiniu momentu, kai kondensatoriaus plokščių įtampa yra didžiausia, iškrovos srovė taip pat yra didžiausia, o sumažėjus Uc iškrovimo metu, iškrovos srovė taip pat mažėja. Kai Uc = 0, iškrovos srovė sustoja.

Išmetimo trukmė priklauso nuo:

1) nuo kondensatoriaus C talpos

2) ant varžos R vertės, iki kurios išsikrauna kondensatorius.

Kuo didesnis pasipriešinimas R, tuo lėčiau vyks iškrova. Taip yra dėl to, kad esant didelei varžai, iškrovos srovės stipris yra mažas, o kondensatoriaus plokščių įkrovos kiekis mažėja lėtai.

Tai galima parodyti to paties kondensatoriaus, kurio talpa 10 μF ir įkraunama iki 100 V įtampos, iškrovimo srovės, esant dviem skirtingoms varžos vertėms (5 pav.): kreivė 1 – ties R. = 40 omų, ioresr = UcО/ R = 100/40 = 2,5 A ir kreivė 2 - esant 20 omų ioresr = 100/20 = 5 A.

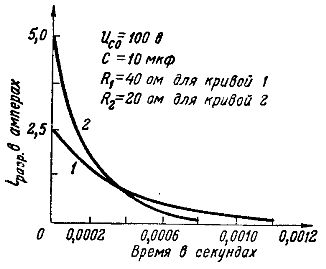
Ryžiai. 5. Skirtingų varžų iškrovos srovių grafikai

Iškrova taip pat yra lėtesnė, kai kondensatoriaus talpa yra didelė.Taip yra todėl, kad esant didesnei kondensatoriaus plokštelių talpai, yra daugiau elektros energijos (daugiau įkrovimo) ir reikės ilgesnio laiko, kol įkrova išsikraus. Tai aiškiai parodo dviejų tos pačios talpos kondensatorių, įkrautų iki vienodos 100 V įtampos ir iškrautų iki varžos R= 40 omų, iškrovos srovių grafikai (6 pav.: 1 kreivė – talpos kondensatoriui 10 mikrofaradų ir 2 kreivė – 20 mikrofaradų talpos kondensatoriui).

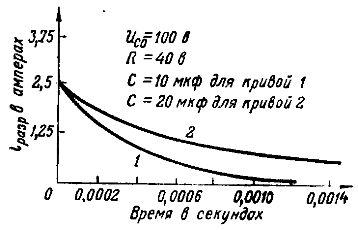
Ryžiai. 6. Skirtingų galių iškrovos srovių grafikai

Iš nagrinėjamų procesų galima daryti išvadą, kad grandinėje su kondensatoriumi srovė teka tik įkrovimo ir iškrovimo momentais, kai keičiasi įtampa ant plokštelių.

Tai paaiškinama tuo, kad keičiantis įtampai keičiasi plokščių krūvio dydis, o tam reikia krūvių judėjimo išilgai grandinės, tai yra, per grandinę turi praeiti elektros srovė. Įkrautas kondensatorius nepraleidžia nuolatinės srovės, nes dielektrikas tarp jo plokščių atidaro grandinę.

Kondensatoriaus energija

Įkrovimo proceso metu kondensatorius kaupia energiją, gaudamas ją iš generatoriaus. Kai kondensatorius išsikrauna, visa elektrinio lauko energija paverčiama šilumos energija, tai yra, ji eina į varžos, per kurią kondensatorius išsikrauna, šildymui. Kuo didesnė kondensatoriaus talpa ir jo plokščių įtampa, tuo didesnė kondensatoriaus elektrinio lauko energija. Energijos kiekis, kurį turi C talpos kondensatorius, įkrautas iki U įtampos, yra lygus: W = Wc = CU2/2

Pavyzdys. Kondensatorius C = 10 μF įkrautas iki Uc = 500 V įtampos.Nustatykite energiją, kuri išsiskirs veikiant šilumos jėgai esant varžai, per kurią iškraunamas kondensatorius.

Atsakymas. Iškrovimo metu visa kondensatoriaus sukaupta energija paverčiama šiluma. Todėl W = Wc = CU2/2 = (10 x 10–6 x 500) / 2 = 1,25 J.