Nešakotosios ir šakotosios linijinės elektros grandinės su vienu tiekimu

Jei daug pasyviųjų elementų kartu su šaltiniu e. ir tt c) sudaro elektros grandinę, jų sujungimas gali būti atliekamas įvairiais būdais. Yra tokios tipinės tokių jungčių schemos.

Elementų nuoseklusis sujungimas Tai paprasčiausias sujungimas. Su šiuo ryšiu visuose grandinės elementuose teka ta pati srovė. Pagal šią schemą gali būti sujungti arba visi pasyvieji grandinės elementai, ir tada grandinė bus viengrandė nešakota (1 pav., a), arba gali būti tik dalis daugiagrandės grandinės elementų. prijungtas.

Jei nuosekliai sujungti n elementų, kuriuose teka ta pati srovė I, tai įtampa grandinės gnybtuose bus lygi n elementų, sujungtų nuosekliai, įtampos kritimų sumai, t.y.

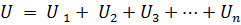
arba:

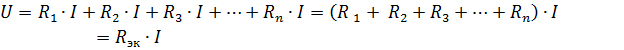
kur Rek yra ekvivalentinė grandinės varža.

Todėl nuosekliai sujungtų pasyviųjų elementų ekvivalentinė varža yra lygi šių elementų varžų sumai... Elektrinė schema (pav.1, a) gali būti pateikta lygiavertė grandinė (1 pav., b), susidedanti iš vieno elemento su lygiaverte varža Rek

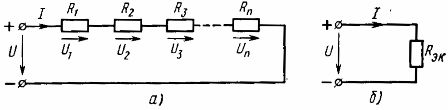
Ryžiai. 1. Linijinių elementų nuoseklaus prijungimo schema (a) ir jai lygiavertė schema (b)

Skaičiuojant grandinę su elementais, sujungtais nuosekliai, esant tam tikrai maitinimo šaltinio įtampai ir elementų varžoms, srovė grandinėje apskaičiuojama pagal Ohmo dėsnį:

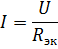
Įtampos kritimas k-ajame elemente

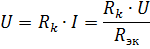
priklauso ne tik nuo šio elemento varžos, bet ir nuo lygiavertės varžos Rek, tai yra nuo kitų grandinės elementų varžos. Tai reikšmingas nuoseklaus elementų sujungimo trūkumas. Ribiniu atveju, kai kurio nors grandinės elemento varža tampa lygi begalybei (atvira grandinė), srovė visuose grandinės elementuose tampa lygi nuliui.

Kadangi, jungiant nuosekliai, srovė visuose grandinės elementuose yra vienoda, elementų įtampos kritimo santykis yra lygus šių elementų varžų santykiui:

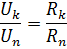
Lygiagretusis elementų sujungimas – tai jungtis, kurioje visiems grandinės elementams taikoma ta pati įtampa. Pagal lygiagretaus jungimo schemą gali būti sujungti arba visi pasyvieji grandinės elementai (2 pav., a), arba tik dalis jų. Kiekvienas lygiagrečiai sujungtas elementas sudaro atskirą šaką. Todėl grandinė su lygiagrečiu elementų prijungimu, parodyta fig. 2, a, nors tai yra paprasta grandinė (kadangi joje yra tik du mazgai), ji tuo pat metu yra šakota.

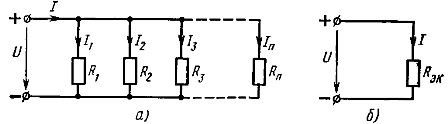
Ryžiai. 2. Linijinių elementų lygiagretaus sujungimo schema (a) ir jai lygiavertė schema (b)

Kiekvienoje lygiagrečioje šakoje srovė

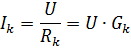
kur Gk – k-osios šakos laidumas.

Nuo Pirmasis Kirchhoffo dėsnis

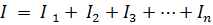
arba

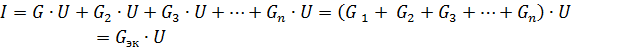
kur Gec yra lygiavertis grandinės laidumas.

Todėl lygiagrečiai sujungus pasyviuosius elementus, jų ekvivalentinis laidumas lygus šių elementų laidų sumai... Ekvivalentinis laidumas visada didesnis už bet kurios lygiagrečių šakų dalies laidumą. Ekvivalentinis laidumas GEK atitinka ekvivalentinę varžą Rek = 1 / Gek.

Tada lygiavertė grandinė, parodyta Fig. 2, a, bus tokios formos, kaip parodyta fig. 2, b. Srovę nešakotoje grandinės dalyje su lygiagrečiu elementų prijungimu galima nustatyti iš šios grandinės pagal Ohmo dėsnį:

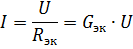
Todėl, jei maitinimo įtampa yra pastovi, tada padidėjus lygiagrečiai sujungtų elementų skaičiui (dėl to padidėja lygiavertis laidumas), srovė nešakotoje grandinės dalyje (maitinimo srovė) didėja.

Iš formulės

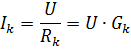
matyti, kad kiekvienoje šakoje srovė priklauso tik nuo tos šakos laidumo ir nepriklauso nuo kitų šakų laidumo. Lygiagrečių šakų režimų nepriklausomumas vienas nuo kito yra svarbus lygiagretaus pasyviųjų elementų sujungimo privalumas. Pramoniniuose įrenginiuose dažniausiai naudojamas lygiagretus elektros imtuvų prijungimas. Ryškiausias pavyzdys yra elektros lempų įtraukimas apšvietimui.

Kadangi lygiagrečiame jungtyje visiems elementams taikoma ta pati įtampa ir kiekvienoje šakoje srovė yra proporcinga tos šakos laidumui, lygiagrečių šakų srovių santykis yra lygus šių šakų laidumo santykiui arba atvirkščiai proporcingas pagal jų varžų santykį:

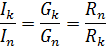
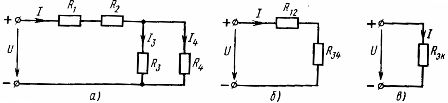
Mišrus elementų sujungimas yra nuoseklių ir lygiagrečių jungčių derinys. Tokia grandinė gali turėti skirtingą mazgų ir šakų skaičių. Mišraus ryšio pavyzdys parodytas diagramoje (3 pav., a)

Ryžiai. 3. Linijinių elementų mišraus sujungimo schema (a) ir jos ekvivalentinės schemos (b, c).

Norint apskaičiuoti tokią grandinę, reikia paeiliui nustatyti lygiavertes varžas toms grandinės dalims, kurios yra tik nuosekliai arba tik lygiagrečiai. Nagrinėjamoje grandinėje yra nuoseklus elementų su varžomis R1 ir R2 sujungimas ir lygiagretus elementų su varžomis R3 ir R4 sujungimas. Naudojant anksčiau gautus ryšius tarp grandinės elementų parametrų su jų nuoseklia ir lygiagrečia jungtimi, reali elektros grandinė gali būti paeiliui pakeista lygiavertėmis grandinėmis.

Ekvivalentinė nuosekliai sujungtų elementų varža

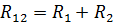
Lygiagrečiai sujungtų elementų R3 ir R4 lygiavertė varža

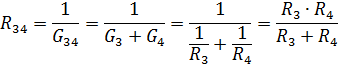
Lygiavertė grandinė su elementų R12 ir R34 varžomis parodyta fig. 3, b. Šiam serijiniam R12 ir R34 prijungimui lygiavertė varža yra

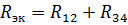
ir atitinkama lygiavertė grandinė parodyta fig. 2, b. Raskime srovę šioje grandinėje:

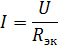
Tai maitinimo srovė ir srovė realiosios grandinės elementuose R1 ir R2.Norėdami apskaičiuoti sroves I3 ir I4, nustatykite įtampą grandinės atkarpoje su varža R34 (3 pav., b):

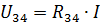
Tada sroves I3 ir I4 galima rasti pagal Ohmo dėsnį:

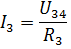
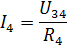
Panašiu būdu galite apskaičiuoti daugybę kitų elektros grandinių su mišriu pasyviųjų elementų prijungimu.

Sudėtingoms grandinėms su daugybe grandinių ir e. ir tt c) toks lygiavertis konvertavimas ne visada gali būti atliktas. Jie apskaičiuojami kitais metodais.