Virpesių procesas elektrotechnikoje ir elektronikoje, virpesių rūšys
Virpesių procesas – įvairaus pakartojamumo laipsnio procesas. Visi virpesių procesai skirstomi į 2 klases: periodinius ir neperiodinius. Teoriškai jie taip pat naudoja tarpinę klasę - beveik periodinius svyravimus.
Virpesinis procesas vadinamas periodiniu, kai šį procesą charakterizuojanti reikšmė, paimta bet kuriuo metu, po tam tikro laiko tarpo T turi tokią pačią reikšmę.
Funkcija f (t), kuri yra matematinė svyravimo proceso išraiška, vadinama periodine su periodu T, jei ji tenkina sąlygą f (t + T) = f (t).
Tarp periodinių virpesių procesų klasės pagrindinį vaidmenį atlieka harmoniniai arba sinusiniai virpesiai, kuriuose fizikinio dydžio pokytis laikui bėgant vyksta pagal sinuso arba kosinuso dėsnį. Bendras jų rekordas yra:
y = f (t) = aCos ((2π / T) t – φ),
čia a — virpesių amplitudė, φ yra virpesių fazė, 1 /T = f — dažnis ir 2πf = ω — ciklinių arba žiedinių virpesių dažnis.
Sinusinių virpesių taikymas ir jų charakteristikos:
Pagrindiniai kintamosios srovės parametrai
Grafiniai kintamosios srovės atvaizdavimo būdai
Beveik periodinė funkcija, atitinkanti periodinių virpesių rodmenis, apibrėžiama sąlyga:
| f · (t + τ) — f (t) | <= ε kur ε – kiekvienai reikšmei T priskirkite reikšmę.
Dydis τ šiuo atveju vadinamas beveik periodu. Jei reikšmė ε yra labai maža, palyginti su vidutine f (t) reikšme momentu T, tai kvaziperiodinė funkcija bus artima periodinei.
Neperiodiniai svyravimai yra daug įvairesni nei periodiniai. Tačiau dažniausiai automatikoje tenka susidurti su slopinamaisiais arba didėjančiais sinusoidiniais svyravimais.
Virpesiai pagal slopinto sinusoido dėsnį arba, kaip kartais vadinami, slopinamuosius harmoninius virpesius, gali būti pavaizduoti bendra forma:
x = Ae-δTcos·(ω + φ),
kur t yra laikas, A ir φ yra savavališkos konstantos. Bendras didėjančių harmoninių virpesių dėsnio žymėjimas skiriasi tik slopinimo koeficiento ženklu δ[1 sekundė].
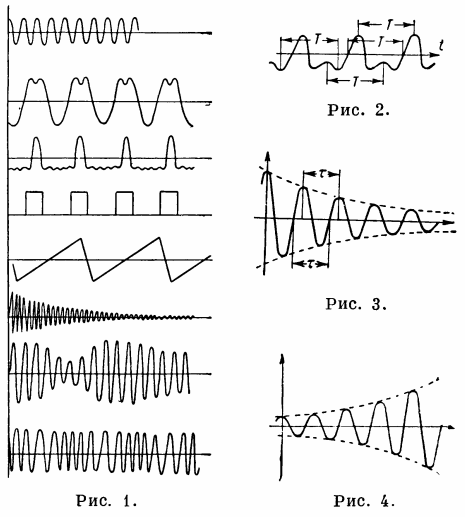
Fig. 1 – svyravimo procesas, pav. 2. — periodinis procesas, pav. 3. — irstantys harmoniniai svyravimai, pav. 4. — harmoninių virpesių padidėjimas.
Virpesių proceso taikymo pavyzdys yra paprasčiausia svyravimo grandinė.
Osciliatoriaus grandinė (elektros grandinė) – pasyvi elektros grandinė, kurioje gali vykti elektriniai virpesiai, kurių dažnis nustatomas pagal pačios grandinės parametrus.
Paprasčiausia virpesių grandinė susideda iš talpos C ir induktyvumo L. Nesant išorinio poveikio, slopinami virpesiai, kurių dažnis εО = 1/2π√LC.
Virpesių amplitudė mažėja, pvz., δT, kur δ yra slopinimo koeficientas. Jei δ> = eO, tai slopinami virpesiai grandinėje tampa neperiodiniai.
Elektronikoje virpesių grandinės kokybę lemia kokybės koeficientas: Q = nf/δ... Kai svyruojančią grandinę veikia išorinė periodinė jėga, joje atsiranda priverstiniai virpesiai. Priverstinių virpesių amplitudė žymiai padidėja aukšto Q grandinėms, jei išorinio poveikio dažnis yra artimas eo (rezonansui). Virpesių grandinė yra viena iš pagrindinių rezonansinių stiprintuvų dalių, generatoriai ir kiti elektroniniai prietaisai.
Taip pat žiūrėkite šia tema: Įtampos rezonanso ir srovės rezonanso taikymas
