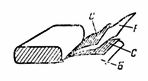
Kondensatoriaus talpos skaičiavimas

Talpa C – tai kondensatoriaus talpa priimti (saugoti ir išlaikyti) elektros kiekį Q ampersekundėmis arba įkrovą Q pakabučiuose. Jei kūnui, pavyzdžiui, rutuliui, pasakysite elektros krūvį (elektros kiekį) Q, tai tarp šio kūno ir žemės prijungtas elektroskopas parodys įtampą U (1 pav.). Ši įtampa yra proporcinga įkrovimui ir taip pat priklauso nuo kūno formos ir dydžio.

Ryšys tarp krūvio Q ir įtampos U išreiškiamas formule Q = C ∙ U.

Proporcingumo konstanta C vadinama kūno talpa. Jei kūnas yra rutulio formos, kūno talpa yra proporcinga rutulio spinduliui r.

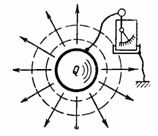
Ryžiai. 1.

Talpos matavimo vienetas yra faradas (F).

Kūno talpa 1 F kai 1 k krūvis sukuria 1 V įtampą tarp jo ir žemės. Faradai yra labai didelis matavimo vienetas, todėl praktikoje naudojami mažesni vienetai: mikrofaradas (μF), nanofaradas (nF) ir pikofaradas (pF)...

Šie vienetai yra susieti šiais santykiais: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

1 cm spindulio rutulio talpa yra 1,1 pF.

Krovinį kaupti gali ne tik izoliuotas kūnas, bet ir specialus prietaisas, vadinamas kondensatoriumi. Kondensatorius susideda iš dviejų ar daugiau plokščių (plokščių), kurios yra atskirtos dielektriku (izoliacija).

Fig. 2 parodyta grandinė su nuolatinės srovės šaltiniu, prijungtu prie kondensatoriaus. Įjungus kondensatoriaus dešinėje plokštelėje susidaro teigiamas krūvis +Q, o kairėje – neigiamas krūvis –Q. Per kondensatoriaus įkrova per grandinę teka srovė, kuri sustoja pasibaigus įkrovimui; tada kondensatoriaus įtampa bus lygi e. ir tt c) šaltinis U. Kondensatoriaus plokštės įkrova, įtampa ir talpa yra susietos santykiu Q = C ∙ U. Tokiu atveju kondensatoriaus dielektrike susidaro elektrostatinis laukas.

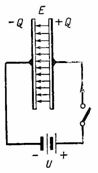
Ryžiai. 2.

Kondensatoriaus su oro dielektriku talpa gali būti apskaičiuojama pagal formulę C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, kur S yra vienos plokštės plotas, cm2; d – atstumas tarp plokščių, cm; C yra kondensatoriaus talpa, pF.

Kondensatoriaus, susidedančio iš n plokštelių, talpa (3 pav.) lygi: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

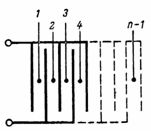
Ryžiai. 3.

Jei tarpas tarp plokščių užpildomas kitu dielektriku, pavyzdžiui, popieriumi, kondensatoriaus talpa padidės ε. Naudojant popierinę izoliaciją, talpa padidės 3 kartus, su žėručio izoliacija - 5-8 kartus, su stiklu - 7 kartus ir kt. ε reikšmė vadinama dielektriko dielektrine konstanta.

Bendra kondensatoriaus, kurio dielektrinė konstanta ε (epsilonas), talpos nustatymo formulė yra tokia: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Ši formulė naudinga apskaičiuojant mažus kintamus radijo imtuvų kondensatorius.Tą pačią formulę galima pavaizduoti taip: C = (ε_0 ∙ ε ∙ S) / d, kur ε_0 yra dielektrinė konstanta arba vakuumo dielektrinė konstanta (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε yra dielektriko dielektrinė konstanta.

Šioje formulėje matmenys pakeičiami metrais, o talpa gaunama faradais.

Pavyzdžiai

1. Kokia yra Žemės planetos, kurios spindulys r = 6378 km, talpa?

Kadangi rutulio, kurio spindulys 1 cm, talpa yra lygi 1,11 pF, Žemės talpa yra: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μ. (Mūsų planetos dydžio rutulio talpa yra palyginti maža. Tokią talpą turi mažo dydžio elektrolitiniai kondensatoriai).

2. Nustatykite kondensatoriaus, susidedančio iš dviejų plokščių, kurių kiekvienos plotas S = 120 cm2, talpą.

Plokštes skiria oro sluoksnis, kurio storis d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Ankstesniame pavyzdyje nurodytais duomenimis nustatykite kondensatoriaus talpą, jei tarpas tarp plokščių užpildytas vaškiniu popieriumi, kurio dielektrinė konstanta ε = 4, stiklu (ε = 7), elektriniu kartonu (ε = 2) , žėrutis (ε = 8 ).

Vaško popieriaus kondensatoriaus talpa C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Stiklinio kondensatoriaus talpa yra C = 7 ∙ 21,2 = 148,4 pF.

Kartoninio kondensatoriaus talpa yra C = 2 ∙ 21,2 = 42,3 pF.

Žėručio kondensatoriaus talpa yra C = 8 ∙ 21,2 = 169,6 pF.

4. Kokia yra oro rotacinio kondensatoriaus talpa radijo imtuvui, susidedančiam iš 20 plokščių, kurių plotas 20 cm2, jei atstumas tarp plokščių yra 0,06 cm (149 pav.)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondensatorius, parodytas fig.3, susideda iš atskirų paprasčiausių kondensatorių su dviem plokštelėmis, kurių skaičius lygus n-1.

5. Popierinis kondensatorius, kurio talpa C = 2 μF, susideda iš dviejų juostelių iš alavo folijos C ir dviejų juostelių dielektriko iš vaško popieriaus B, kurio dielektrinė konstanta ε = 6. Vaško popieriaus storis d = 0,1 mm. Sulenktos juostelės suvyniotos, laidai pagaminti iš plieninių plokščių. Nustatykite kondensatoriaus plieno juostos ilgį, jei jos plotis yra 4 cm (4 pav.).

Ryžiai. 4.

Pirmiausia nustatome vienos juostos plotą pagal formulę C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, iš kur S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Kiekvienos juostos ilgis l = 37680/4 = 9420 cm = 94,2 m.