AC kondensatorius

Surinkime grandinę su kondensatorius, kur generatorius generuoja sinusinę įtampą. Išanalizuokime nuosekliai, kas atsitiks grandinėje, kai uždarysime jungiklį. Atsižvelgsime į pradinį momentą, kai generatoriaus įtampa lygi nuliui.

Per pirmąjį laikotarpio ketvirtį generatoriaus gnybtų įtampa padidės, pradedant nuo nulio, ir kondensatorius pradės krauti. Grandinėje atsiras srovė, tačiau pirmuoju kondensatoriaus įkrovimo momentu, nepaisant to, kad įtampa ant jo plokščių ką tik pasirodė ir vis dar yra labai maža, srovė grandinėje (įkrovimo srovė) bus didžiausia . Didėjant kondensatoriaus įkrovimui, srovė grandinėje mažėja ir pasiekia nulį tuo momentu, kai kondensatorius yra visiškai įkrautas. Šiuo atveju kondensatoriaus plokščių įtampa, griežtai laikanti generatoriaus įtampą, šiuo metu tampa maksimali, tačiau su priešingu ženklu, tai yra, ji nukreipta į generatoriaus įtampą.

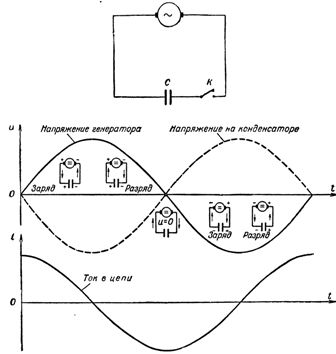
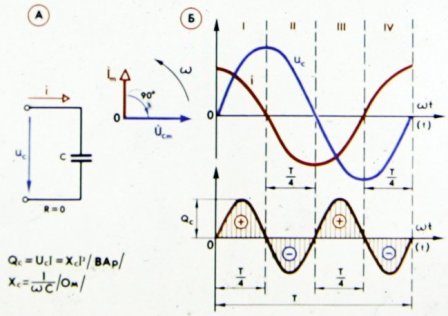
Ryžiai. 1. Srovės ir įtampos pokytis grandinėje su talpa

Tokiu būdu srovė su didžiausia jėga veržiasi į kondensatorių nemokamai, bet iš karto pradeda mažėti, kai kondensatoriaus plokštės prisipildo krūvių ir nukrenta iki nulio, visiškai jį įkraunant.

Palyginkime šį reiškinį su tuo, kas nutinka vandens tekėjimui vamzdyje, jungiančiame du susisiekiančius indus (2 pav.), kurių vienas pilnas, o kitas tuščias. Tereikia paspausti vožtuvą, blokuojantį vandens kelią, nes vanduo iš kairiojo indo, esant dideliam slėgiui, tuoj pat per vamzdį patenka į tuščią dešinįjį indą. Tačiau iš karto vandens slėgis vamzdyje palaipsniui pradės silpti dėl lygių induose išlyginimo ir nukris iki nulio. Vandens tekėjimas sustos.

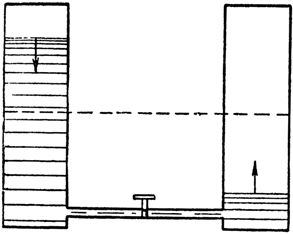
Ryžiai. 2. Vandens slėgio pokytis vamzdyje, jungiančiame ryšių indus, yra panašus į srovės pasikeitimą grandinėje įkraunant kondensatorių.

Panašiai srovė pirmiausia patenka į neįkrautą kondensatorių, o po to palaipsniui susilpnėja kraunant.

Prasidėjus antrajam laikotarpio ketvirčiui, kai generatoriaus įtampa iš pradžių paleidžiama lėtai, o vėliau vis sparčiau mažėja, įkrautas kondensatorius išsikraus į generatorių, sukeldamas iškrovos srovę grandinėje. Mažėjant generatoriaus įtampai, kondensatorius vis labiau išsikrauna, o iškrovos srovė grandinėje didėja. Iškrovos srovės kryptis šiame laikotarpio ketvirtyje yra priešinga įkrovimo srovės krypčiai pirmąjį laikotarpio ketvirtį. Atitinkamai, dabartinė kreivė, pralenkusi nulinę reikšmę, dabar yra žemiau laiko ašies.

Pasibaigus pirmajam pusciklui generatoriaus, taip pat kondensatoriaus įtampa greitai artėja prie nulio, o grandinės srovė pamažu pasiekia maksimalią vertę. Atsižvelgiant į tai, kad srovės vertė grandinėje yra didesnė, tuo didesnė grandinėje nešamo krūvio vertė, paaiškės, kodėl srovė pasiekia maksimalią įtampą ant kondensatoriaus plokščių, taigi ir įkrova. kondensatorius, greitai mažėja.

Prasidėjus trečiajam laikotarpio ketvirčiui, kondensatorius vėl pradeda krauti, tačiau keičiasi jo plokščių poliškumas, taip pat generatoriaus poliškumas „ir atvirkščiai, o srovė teka ta pačia kryptimi. kryptimi, pradeda mažėti kondensatoriui įsikraunant.. Trečiojo laikotarpio ketvirčio pabaigoje generatoriaus ir kondensatoriaus įtampai pasiekus maksimalią, srovė pereina į nulį.

Per paskutinį laikotarpio ketvirtį įtampa, mažėjant, nukrenta iki nulio, o srovė, pakeitusi kryptį grandinėje, pasiekia maksimalią vertę. Čia baigiasi laikotarpis, po kurio prasideda kitas, tiksliai pakartojant ankstesnįjį ir pan.

Taigi, veikiant kintamajai generatoriaus įtampai, kondensatorius per laikotarpį įkraunamas du kartus (pirmasis ir trečiasis laikotarpio ketvirtis) ir du kartus iškraunamas (antrasis ir ketvirtasis laikotarpio ketvirtis). Bet kadangi jie keičiasi po vieną kondensatorių įkrovimas ir iškrovimas kiekvieną kartą kartu su įkrovimo ir iškrovimo srovės pratekėjimu per grandinę, tada galime daryti išvadą kintamoji srovė.

Tai galite patikrinti atlikdami šį paprastą eksperimentą. Prijunkite 4–6 mikrofaradų kondensatorių prie elektros tinklo per 25 W lemputę.Lemputė užsidegs ir neužges, kol nenutrūks grandinė. Tai rodo, kad per grandinę su talpa praėjo kintamoji srovė. Žinoma, jis nepraeina per kondensatoriaus dielektriką, bet bet kuriuo momentu reiškia įkrovimo srovę arba kondensatoriaus iškrovimo srovę.

Kaip žinome, dielektrikas yra poliarizuotas veikiant jame atsirandančiam elektriniam laukui, kai kondensatorius įkraunamas, o jo poliarizacija išnyksta, kai kondensatorius išsikrauna.

Šiuo atveju dielektrikas su jame kylančia poslinkio srove tarnauja kintamajai srovei kaip tam tikras grandinės tęsinys, o konstantai jis nutraukia grandinę. Tačiau poslinkio srovė susidaro tik kondensatoriaus dielektrike, todėl krūviai neperkeliami grandinėje.

Kintamosios srovės kondensatoriaus varža priklauso nuo kondensatoriaus talpos vertės ir srovės dažnio.

Kuo didesnė kondensatoriaus talpa, tuo didesnis grandinės įkrovimas kondensatoriaus įkrovimo ir iškrovimo metu ir, atitinkamai, tuo didesnė srovė grandinėje. Srovės padidėjimas grandinėje rodo, kad jos varža sumažėjo.

Todėl, didėjant talpai, grandinės varža kintamajai srovei mažėja.

Tai auga srovės dažnis padidina grandinėje nešamo krūvio kiekį, nes kondensatoriaus įkrovimas (taip pat ir iškrovimas) turi vykti greičiau nei esant žemam dažniui. Tuo pačiu metu perkelto krūvio padidėjimas per laiko vienetą yra lygus srovės padidėjimui grandinėje, taigi ir jos atsparumo sumažėjimui.

Jei kažkaip palaipsniui sumažinsime kintamosios srovės dažnį ir sumažinsime srovę iki nuolatinės srovės, tai į grandinę įtraukto kondensatoriaus varža palaipsniui didės ir taps be galo didelė (nutrauks grandinę), kol pasirodys nuolatinės srovės grandinė.

Todėl, didėjant dažniui, kondensatoriaus varža kintamajai srovei mažėja.

Kaip ritės varža kintamajai srovei vadinama indukcine, taip ir kondensatoriaus varža vadinama talpine.

Todėl talpinė varža yra didesnė, tuo mažesnė grandinės talpa ir ją maitinančios srovės dažnis.

Talpinė varža žymima Xc ir matuojama omais.

Talpinės varžos priklausomybė nuo srovės dažnio ir grandinės talpos nustatoma pagal formulę Xc = 1 /ωC, kur ω yra apskritimo dažnis, lygus 2πe sandaugai, C yra grandinės talpa faradai.

Talpinė varža, kaip ir indukcinė varža, turi reaktyvų pobūdį, nes kondensatorius nevartoja srovės šaltinio energijos.

formulę Omo dėsnis talpinei grandinei ji turi formą I = U / Xc, kur I ir U - efektyvios srovės ir įtampos vertės; Xc yra grandinės talpinė varža.

Ryšio įrangos grandinėse plačiai naudojama kondensatorių savybė užtikrinti didelį atsparumą žemo dažnio srovėms ir lengvai praleisti aukšto dažnio sroves.

Kondensatorių pagalba, pavyzdžiui, pasiekiamas nuolatinių ir žemo dažnio srovių atskyrimas nuo aukšto dažnio srovių, būtinų grandinių veikimui.

Jei reikia blokuoti žemo dažnio srovės kelią aukšto dažnio grandinės dalyje, nuosekliai jungiamas mažas kondensatorius. Jis pasižymi dideliu atsparumu žemo dažnio srovei ir tuo pačiu lengvai praleidžia aukšto dažnio srovę.

Jei reikia užkirsti kelią aukšto dažnio srovei, pavyzdžiui, radijo stoties maitinimo grandinėje, tada naudojamas didelės talpos kondensatorius, prijungtas lygiagrečiai su srovės šaltiniu. Šiuo atveju aukšto dažnio srovė praeina per kondensatorių, aplenkdama radijo stoties maitinimo grandinę.

Aktyvioji varža ir kondensatorius kintamosios srovės grandinėje

Praktikoje dažnai pastebimi atvejai, kai yra nuoseklioje grandinėje su talpa įtrauktas aktyvusis pasipriešinimas. Bendra grandinės varža šiuo atveju nustatoma pagal formulę

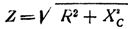
Todėl visos grandinės, susidedančios iš aktyviosios ir talpinės kintamosios srovės varžos, varža yra lygi šios grandinės aktyviosios ir talpinės varžos kvadratų sumos kvadratinei šaknims.

Omo dėsnis galioja ir šiai I = U / Z grandinei.

Fig. 3 parodytos kreivės, apibūdinančios fazių ryšį tarp srovės ir įtampos grandinėje, kurioje yra talpinė ir aktyvioji varža.

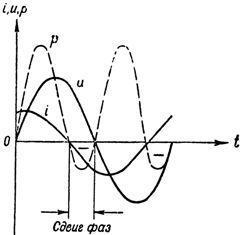
Ryžiai. 3. Srovė, įtampa ir galia grandinėje su kondensatoriumi ir aktyvia varža

Kaip matyti iš paveikslo, srovė šiuo atveju padidina įtampą ne ketvirtadaliu periodo, o mažiau, nes aktyvioji varža pažeidžia grynai talpinį (reaktyvųjį) grandinės pobūdį, kaip rodo sumažėjusi fazė. pamaina. Dabar įtampa grandinės gnybtuose apibrėžiama kaip dviejų komponentų suma: įtampos reaktyvusis komponentas įveiks grandinės talpinę varžą ir aktyvųjį įtampos komponentą, įveikdamas jo aktyviąją varžą.

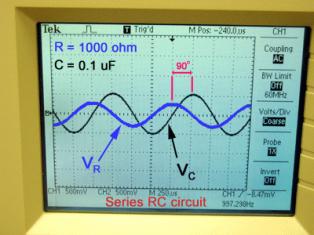
Kuo didesnė grandinės aktyvioji varža, tuo mažesnis fazės poslinkis tarp srovės ir įtampos.

Galios kitimo grandinėje kreivė (žr. 3 pav.) du kartus per laikotarpį įgavo neigiamą ženklą, o tai, kaip jau žinome, yra grandinės reaktyviosios prigimties pasekmė. Kuo mažiau reaktyvi grandinė, tuo mažesnis fazės poslinkis tarp srovės ir įtampos ir tuo daugiau srovės šaltinio energijos ta grandinė sunaudoja.

Taip pat skaitykite: Įtampos rezonansas